Математическое программирование 03
Контрольная работа оформляется в виде файла в Word, с приложением решения 2-й задачи в Excel. Рисунок к 1-й задаче может быть выполнен вручную, сканирован и приложен отдельно или вставлен в текст контрольной. (Выбираете по порядковому номеру в списке группы)
Вариант 2.
1. Решить задачу линейного программирования графическим методом: Найти F = 2x1 - x2 ® min при ограничениях

![]() .
.
Необходимо найти минимальное значение целевой функции F = 2x1-x2 → min, при системе ограничений:
|
X1+x2≥4 |
(1) |
|
-x1+2x2≤2 |
(2) |
|
X1+2x2≤10 |
(3) |
|
X1≥0 |
(4) |
|
X2≥0 |
(5) |
Построим область допустимых решений, т. е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
Построим уравнение x1+x2=4 По двум точкам.
Для нахождения первой точки приравниваем x1=0. Находим x2=4. Для нахождения второй точки приравниваем x2=0. Находим x1=4. Соединяем точку (0;4) с (4;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 1•0 +1•0-4≤0, т. е. x1+x2 - 4≥ 0 в полуплоскости выше прямой.
Построим уравнение - x1+2x2=2 По двум точкам.
Для нахождения первой точки приравниваем x1=0. Находим x2=1. Для нахождения второй точки приравниваем x2=0. Находим x1=-2. Соединяем точку (0;1) с (-2;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: -1•0+2•0-2≤0, т. е. - x1+2x2-2≤ 0 в полуплоскости ниже прямой.
Построим уравнение x1+2x2=10 По двум точкам.
Для нахождения первой точки приравниваем x1=0. Находим x2=5. Для нахождения второй точки приравниваем x2=0. Находим x1=10. Соединяем точку (0;5) с (10;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 1•0+2•0-10≤0, т. е. x1+2x2-10≤0 в полуплоскости ниже прямой.
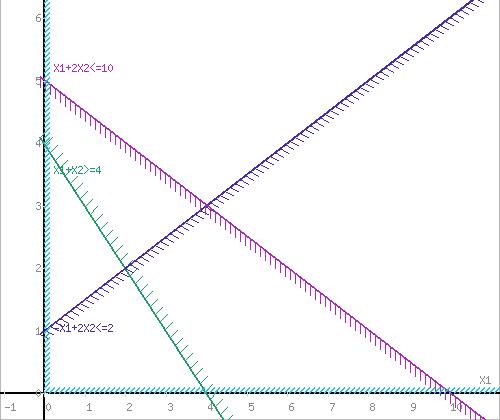
Границы области допустимых решений
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Рассмотрим целевую функцию задачи F=2x1-x2→min.
Построим прямую, отвечающую значению функции F=0: F=2x1-x2=0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора – точка (0;0), конец – точка (2;-1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых:
X1+x2=4
-x1+2x2=2
Решив систему уравнений, получим: X1=2, x2=2
Откуда найдем минимальное значение целевой функции:
F(X)=2*2-1*2=2
Ответ: x1 = 2, x2 = 2, F(X) = 2
2. Решить задачу симплекс-методом и проверить решение, используя программное средство Excel (команду «поиск решения»):

Решение
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 6x1 + x2 - x3 - 2x4 при следующих условиях-ограничений.
X1 + 2x2 + x3 + 6x4 + x5=4
3x1 - x2 - 3x3 + x4=1
X1 + 3x2 + 5x3=9
Введем Искусственные переменные x: в 1-м равенстве переменную x5 принимаем в качестве базисной; в 2-м равенстве вводим переменную x6; в 3-м равенстве вводим переменную x7;
1x1 + 2x2 + 1x3 + 6x4 + 1x5 + 0x6 + 0x7 = 4
3x1-1x2-3x3 + 1x4 + 0x5 + 1x6 + 0x7 = 1
1x1 + 3x2 + 5x3 + 0x4 + 0x5 + 0x6 + 1x7 = 9
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = 6x1+x2-1x3-2x4 - Mx6 - Mx7 → max
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные:
x6 = 1-3x1+x2+3x3-x4
X7 = 9-x1-3x2-5x3
Которые подставим в целевую функцию:
F(X) = 6x1 + x2-x3-2x4 - M(1-3x1+x2+3x3-x4) - M(9-x1-3x2-5x3) → max
Или F(X) = (6+4M)x1+(1+2M)x2+(-1+2M)x3+(-2+M)x4+(-10M) → max
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
|
1 |
2 |
1 |
6 |
1 |
0 |
0 |
|
3 |
-1 |
-3 |
1 |
0 |
1 |
0 |
|
1 |
3 |
5 |
0 |
0 |
0 |
1 |
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Экономический смысл дополнительных переменных: дополнительные переменные задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Решим систему уравнений относительно базисных переменных: x5, x6, x7
Полагая, что Свободные переменные равны 0, получим первый опорный план: X1 = (0,0,0,0,4,1,9).
Базисное решение называется допустимым, если оно неотрицательно.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X5 |
4 |
1 |
2 |
1 |
6 |
1 |
0 |
0 |
|
X6 |
1 |
3 |
-1 |
-3 |
1 |
0 |
1 |
0 |
|
X7 |
9 |
1 |
3 |
5 |
0 |
0 |
0 |
1 |
|
F(X0) |
-10M |
-6-4M |
-1-2M |
1-2M |
2-M |
0 |
0 |
0 |
Переходим к основному алгоритму симплекс-метода.
Итерация №0.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее: min (4 : 1 , 1 : 3 , 9 : 1 ) = 1/3
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
Min |
|
X5 |
4 |
1 |
2 |
1 |
6 |
1 |
0 |
0 |
4 |
|
X6 |
1 |
3 |
-1 |
-3 |
1 |
0 |
1 |
0 |
1/3 |
|
X7 |
9 |
1 |
3 |
5 |
0 |
0 |
0 |
1 |
9 |
|
F(X1) |
-10M |
-6-4M |
-1-2M |
1-2M |
2-M |
0 |
0 |
0 |
0 |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x6 в план 1 войдет переменная x1.
Строка, соответствующая переменной x1 в плане 1, получена в результате деления всех элементов строки x6 плана 0 на разрешающий элемент РЭ=3
На месте разрешающего элемента в плане 1 получаем 1.
В остальных клетках столбца x1 плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x1 и столбец x1.
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ,
СТЭ - элемент старого плана, РЭ - разрешающий элемент (3), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Получаем новую симплекс-таблицу:
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X5 |
11/3 |
0 |
7/3 |
2 |
17/3 |
1 |
-1/3 |
0 |
|
X1 |
1/3 |
1 |
-1/3 |
-1 |
1/3 |
0 |
1/3 |
0 |
|
X7 |
26/3 |
0 |
10/3 |
6 |
-1/3 |
0 |
-1/3 |
1 |
|
F(X1) |
2-82/3M |
0 |
-3-31/3M |
-5-6M |
4+M |
0 |
2+11/3M |
0 |
Итерация №1.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai3
и из них выберем наименьшее: min (32/3 : 2 , - , 82/3 : 6 ) = 14/9
Следовательно, 3-ая строка является ведущей.
Разрешающий элемент равен (6) и находится на пересечении ведущего столбца и ведущей строки.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
Min |
|
X5 |
32/3 |
0 |
21/3 |
2 |
52/3 |
1 |
-1/3 |
0 |
15/6 |
|
X1 |
1/3 |
1 |
-1/3 |
-1 |
1/3 |
0 |
1/3 |
0 |
- |
|
X7 |
82/3 |
0 |
31/3 |
6 |
-1/3 |
0 |
-1/3 |
1 |
14/9 |
|
F(X2) |
2-82/3M |
0 |
-3-31/3M |
-5-6M |
4+M |
0 |
2+11/3M |
0 |
0 |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x7 в план 2 войдет переменная x3.
Строка, соответствующая переменной x3 в плане 2, получена в результате деления всех элементов строки x7 плана 1 на разрешающий элемент РЭ=6
На месте разрешающего элемента в плане 2 получаем 1.
В остальных клетках столбца x3 плана 2 записываем нули.
Таким образом, в новом плане 2 заполнены строка x3 и столбец x3.
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую симплекс-таблицу:
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X5 |
7/9 |
0 |
11/9 |
0 |
52/9 |
1 |
-2/9 |
-1/3 |
|
X1 |
16/9 |
1 |
2/9 |
0 |
5/18 |
0 |
5/18 |
1/6 |
|
X3 |
13/9 |
0 |
5/9 |
1 |
-1/18 |
0 |
-1/18 |
1/6 |
|
F(X2) |
92/9 |
0 |
-2/9 |
0 |
313/18 |
0 |
113/18+M |
5/6+M |
Итерация №2.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai2
и из них выберем наименьшее: min (7/9 : 12/9 , 17/9 : 2/9 , 14/9 : 5/9 ) = 7/11
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (12/9) и находится на пересечении ведущего столбца и ведущей строки.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
Min |
|
X5 |
7/9 |
0 |
12/9 |
0 |
57/9 |
1 |
-2/9 |
-1/3 |
7/11 |
|
X1 |
17/9 |
1 |
2/9 |
0 |
5/18 |
0 |
5/18 |
1/6 |
8 |
|
X3 |
14/9 |
0 |
5/9 |
1 |
-1/18 |
0 |
-1/18 |
1/6 |
23/5 |
|
F(X3) |
92/9 |
0 |
-2/9 |
0 |
313/18 |
0 |
113/18+M |
5/6+M |
0 |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x5 в план 3 войдет переменная x2.
Строка, соответствующая переменной x2 в плане 3, получена в результате деления всех элементов строки x5 плана 2 на разрешающий элемент РЭ=12/9
На месте разрешающего элемента в плане 3 получаем 1.
В остальных клетках столбца x2 плана 3 записываем нули.
Таким образом, в новом плане 3 заполнены строка x2 и столбец x2.
Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую симплекс-таблицу:
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X2 |
7/11 |
0 |
1 |
0 |
52/11 |
9/11 |
-2/11 |
-3/11 |
|
X1 |
18/11 |
1 |
0 |
0 |
-17/22 |
-2/11 |
7/22 |
5/22 |
|
X3 |
12/11 |
0 |
0 |
1 |
-59/22 |
-5/11 |
1/22 |
7/22 |
|
F(X3) |
94/11 |
0 |
0 |
0 |
417/22 |
2/11 |
115/22+M |
17/22+M |
1. Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X2 |
7/11 |
0 |
1 |
0 |
52/11 |
9/11 |
-2/11 |
-3/11 |
|
X1 |
18/11 |
1 |
0 |
0 |
-17/22 |
-2/11 |
7/22 |
5/22 |
|
X3 |
12/11 |
0 |
0 |
1 |
-59/22 |
-5/11 |
1/22 |
7/22 |
|
F(X4) |
94/11 |
0 |
0 |
0 |
417/22 |
2/11 |
115/22+M |
17/22+M |
Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым.
Оптимальный план можно записать так:
X2 = 7/11
X1 = 17/11
X3 = 11/11
F(X) = 1•7/11 + 6•17/11 -1•11/11 = 94/11
Ответ: x2 = 7/11, x1 = 17/11, x3 = 11/11, F(X) = 94/11
| < Предыдущая | Следующая > |
|---|