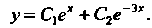26.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Уравнение вида
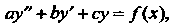 (26.7)
(26.7)
Где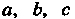 - постоянные
- постоянные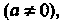 Называется дифференциальным уравнением
Называется дифференциальным уравнением
Второго порядка с постоянными коэффициентами.
Если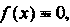 То уравнение (26.7) называется линейным однородным диффе
То уравнение (26.7) называется линейным однородным диффе
Ренциальным уравнением с постоянными коэффициентами или уравнением без правой части: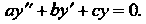
Последнее уравнение можно привести к виду
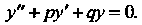 (26.8)
(26.8)
Уравнение
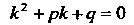 (26.9)
(26.9)
Называется характеристическим уравнением для уравнения (26.8).
В зависимости от корней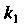 И
И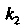 Характеристического уравнения (26.9) получаем общее решение уравнения (26.8) в виде
Характеристического уравнения (26.9) получаем общее решение уравнения (26.8) в виде
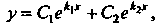 (26.10)
(26.10)
Если корни действительны и различны;
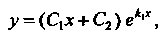 (26.11)
(26.11)
Если корни действительны и равны;
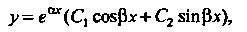 (26.12)
(26.12)
Если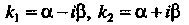 - комплексные числа.
- комплексные числа.
Пример 26.4. Проинтегрировать дифференциальное уравнение 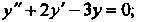 Найти частное решение, удовлетворяющее условиям:
Найти частное решение, удовлетворяющее условиям: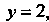
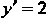 При
При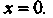
Характеристическое уравнение (26.9) для данного уравнения принимает вид 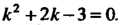 Так как
Так как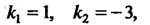 То общее решение в соответствии с
То общее решение в соответствии с
(26.10) определяется формулой
Чтобы найти указанное частное решение, подставим начальные данные х = 0, 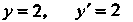 В выражения для
В выражения для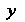 И
И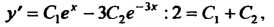
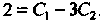 , Из этой системы находим
, Из этой системы находим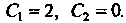 При этих значениях
При этих значениях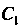 И
И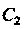 Функция (1) принимает вид
Функция (1) принимает вид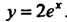 Итак,
Итак,
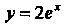 — искомое частное решение.
— искомое частное решение.
Пример 26.5. Проинтегрировать уравнение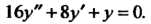
Характеристическое уравнение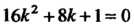 Имеет два равных корня
Имеет два равных корня
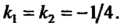 Общее решение данного дифференциального уравнения в соответствии с (26.11) определяется формулой
Общее решение данного дифференциального уравнения в соответствии с (26.11) определяется формулой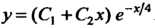
П р^и м е р 26.6. Найти общее решение уравнения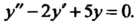
Характеристическое уравнение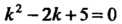 Имеет комплексные корни
Имеет комплексные корни
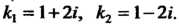 Общее решение определяется формулой (26.12), в которой
Общее решение определяется формулой (26.12), в которой
Нужно положить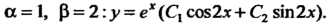 I Пример 26.7. Решить уравнение
I Пример 26.7. Решить уравнение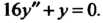 Характеристическое уравнение
Характеристическое уравнение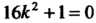 Имеет чисто мнимые корни
Имеет чисто мнимые корни
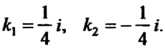 Пользуясь формулой (26.12), полагая в ней
Пользуясь формулой (26.12), полагая в ней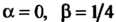 получаем общее решение
получаем общее решение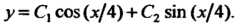
| < Предыдущая | Следующая > |
|---|