26.3. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Если в уравнении (26.7)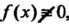 , то оно называется неоднородным диффе
, то оно называется неоднородным диффе
Ренциальным уравнением второго порядка с постоянными коэффициентами; это уравнение может быть приведено к виду
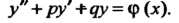 (26.13)
(26.13)
Общее решение уравнения (26.13) определяется формулой
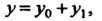 (26.14)
(26.14)
Где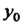 — общее решение соответствующего однородного уравнения
— общее решение соответствующего однородного уравнения
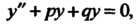 А
А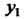 - частное решение уравнения (26.13).
- частное решение уравнения (26.13).
В простейших случаях, когда функция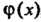 , входящая в уравнение (26.13),
, входящая в уравнение (26.13),
Является показательной или многочленом, указанное частное решение находится с помощью метода неопределенных коэффициентов.
Если
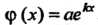 (26.15)
(26.15)
Где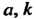 - постоянные, то частное решение уравнения (26.13) ищут в виде
- постоянные, то частное решение уравнения (26.13) ищут в виде
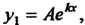 (26.16)
(26.16)
Когда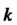 Не является корнем характеристического уравнения или в виде
Не является корнем характеристического уравнения или в виде 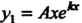 , когда
, когда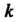 — простой корень характеристического уравнения, или
— простой корень характеристического уравнения, или 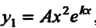 .когда
.когда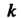 - кратный корень указанного уравнения.
- кратный корень указанного уравнения.
Виде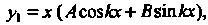 Когда
Когда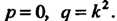
Если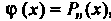 , где
, где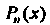 - многочлен степени
- многочлен степени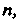 То частное решение
То частное решение
Уравнения (26.13) ищут в виде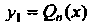 В случае, когда
В случае, когда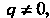 И в виде
И в виде
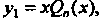 Когда
Когда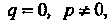 Где
Где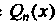 — многочлен степени
— многочлен степени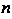 .
.
Пусть дано неоднородное уравнение
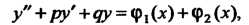 (26.17)
(26.17)
Правая часть которого есть сумма двух функций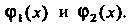 Если
Если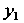 Является
Является
Частным решением уравнения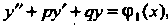 , а
, а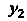 — частным решением
— частным решением
Уравнения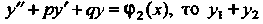 - частное решение уравнения (26.17).
- частное решение уравнения (26.17).
Пример 26.8. Проинтегрировать уравнение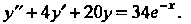 Найдем сначала общее решение соответствующего однородного уравнения
Найдем сначала общее решение соответствующего однородного уравнения 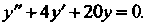 . Характеристическое уравнение
. Характеристическое уравнение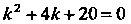 Имеет корни
Имеет корни
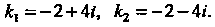 Следовательно, общее решение однородного уравнения
Следовательно, общее решение однородного уравнения
Определяется формулой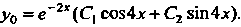
Переходим к отысканию частного решения исходного уравнения. Так как в данном случае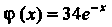 (т. е. имеет вид (26.15):
(т. е. имеет вид (26.15):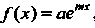 , где
, где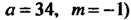 и
и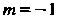 Не является корнем характеристического уравнения, то в соответствии с формулой (26.16) ищем частное решение в виде
Не является корнем характеристического уравнения, то в соответствии с формулой (26.16) ищем частное решение в виде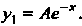 Находя производные этой функции
Находя производные этой функции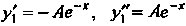 И подставляя выражения для
И подставляя выражения для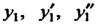 В исходное уравнение, получаем
В исходное уравнение, получаем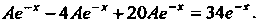 Так как
Так как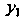 -решение уравнения, то последнее равенство выполняется для всех
-решение уравнения, то последнее равенство выполняется для всех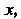 Т. е. является тождеством:
Т. е. является тождеством: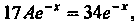 , откуда
, откуда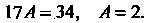 Следовательно, частное решение имеет вид
Следовательно, частное решение имеет вид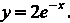 На основании формулы (26.14) получаем общее решение
На основании формулы (26.14) получаем общее решение
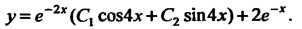
Пример 26.9. Найти общее решение уравнения 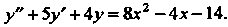 Правая часть данного уравнения является полиномом второй степени
Правая часть данного уравнения является полиномом второй степени
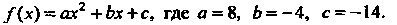
Так как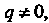 То частное решение ищем в виде
То частное решение ищем в виде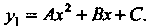 Подставляя вы
Подставляя вы
Ражения для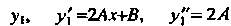 В данное уравнение, получаем
В данное уравнение, получаем
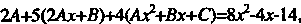 , или
, или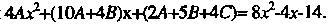
Поскольку у, - решение дифференциального уравнения, то последнее равенство должно выполняться при всех х, т. е. являться тождеством, поэтому коэффи-
Циенты при одинаковых степенях х, стоящие в разных частях, равны между собой:
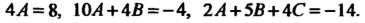
Из полученной системы уравнений находим, что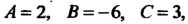 По
По
Этому j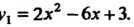 Общее решение соответствующего однородного уравне
Общее решение соответствующего однородного уравне
Ния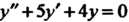 Определяется формулой
Определяется формулой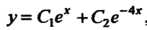 ,^так как. характе
,^так как. характе
Ристическое уравнение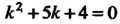 Имеет корни
Имеет корни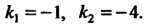
На основании формулы (26.14) получаем общее решение
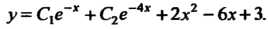
Пример 26.10. Проинтегрировать уравнение
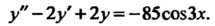
Это уравнение вида (26.13), где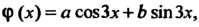 Причем
Причем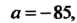
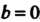 . Частное решение данного уравнения ищем в виде
. Частное решение данного уравнения ищем в виде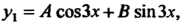 тогда
тогда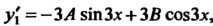
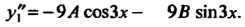 Подставив эти
Подставив эти
Выражения в исходное уравнение, получим тождество
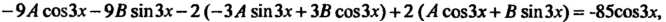
Или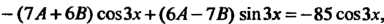 Откуда
Откуда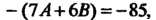
(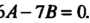 Решив последнюю систему уравнений, найдем, что
Решив последнюю систему уравнений, найдем, что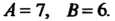
Следовательно,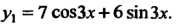
Общее решение соответствующего однородного уравнения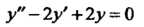 определяется формулой
определяется формулой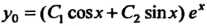 (см. (26.12)), так как характе
(см. (26.12)), так как характе
Ристическое уравнение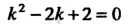 Имеет комплексные корни
Имеет комплексные корни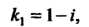
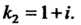 На основании формулы (26.14) получаем общее решение
На основании формулы (26.14) получаем общее решение
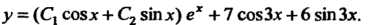
Пример 26.11. Проинтегрировать уравнение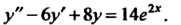 Соответствующее однородное уравнение
Соответствующее однородное уравнение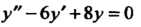 Имеет общее решение
Имеет общее решение
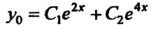 (получено по формуле (26.10), ибо
(получено по формуле (26.10), ибо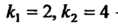 - различные
- различные
Действительные корни характеристического уравнения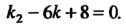 Исходное
Исходное
Уравнение является уравнением вида (26.13), где функция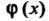 Определяется формулой (26.15), причем
Определяется формулой (26.15), причем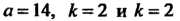 - корень характеристического уравнения.
- корень характеристического уравнения.
Частное решение данного неоднородного уравнения в этом случае следует искать в виде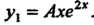 Так как
Так как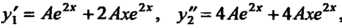 , то подстановка выражения для
, то подстановка выражения для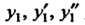 .в исходное уравнение приводит к тождеству
.в исходное уравнение приводит к тождеству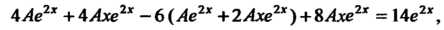 Или
Или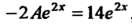 , откуда
, откуда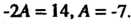 Таким образом,
Таким образом,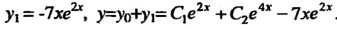
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
| < Предыдущая | Следующая > |
|---|