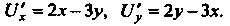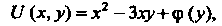25.4. Уравнения в полных дифференциалах

Уравнением в полных дифференциалах называется уравнение

Левая часть которого является полным дифференциалом некоторой функции, т. е.

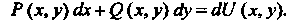(25.9)

Общий интеграл уравнения (25.8) определяется формулой

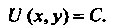(25.10)

Поскольку

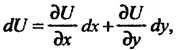(25.11)

То из равенств (25.9) и (25.11) следуют уравнения

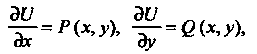(25.12)

Которыми определяется функция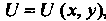, входящая в формулу (25.10).

Необходимое и достаточное условие того, что уравнение (25.8) является уравнением в полных дифференциалах, выражается равенством

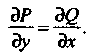(25.13)

Если левая часть уравнения (25.8) не является полным дифференциалом, но становится таковым при умножении на некоторую функцию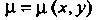

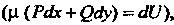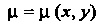ТоНазывается интегрирующим множителем.

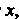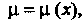Интегрирующий множитель зависит только отТ. е.Если

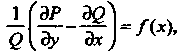
И зависит только от у, если

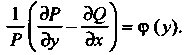
Пример 25.4. Проинтегрировать дифференциальное уравнение 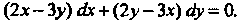 Для данного уравнения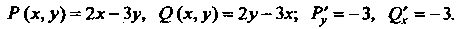

Так как выполнено условие (25.13), то данное уравнение является уравнением в полных дифференциалах; следовательно, равенства (2S. 12) принимают вид

(1)

Интегрируя первое из этих уравнений (При этом считается постоянным), находим

(2)

Где- функция, подлежащая определению.

Дифференцируя по у функциюИ принимая во внимание второе из

Равенств (1), получаем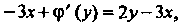Откуда

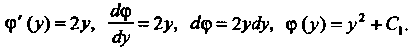
Подставив выражение для <р (у) в равенство (2), найдем

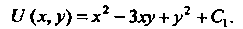
В соответствии с формулой (25.10) получаем

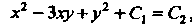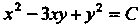, или, где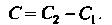

Итак, _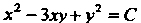- общий интеграл данного уравнения.

Замечание. Это уравнение является также однородным; его можно проинтегрировать с помощью формулы (25.4).

< Предыдущая		Следующая >