20. Отображения множеств
Пусть X и Y — два непустых множества.
Отображением f: X →Y (множества X во множество Y) называется тройка (X, Y, F). Здесь X, Y — два непустых множества, F – правило, сопоставляющее каждому элементу Х ϵ X однозначно определенный элемент У = f(x) ϵ Y. Множество X называется Областью определения Отображения, элемент Х ϵ X – Аргументом отображения F, элемент F(x) ϵ Y –Образом элемента Х при отображении F. При этом пишут Х → f(x). Часто, в случае когда множества X, Y –числовые, отображение называют Функцией. Если только множество Y– числовое, то отображение называют Функционалом.
Если А ![]() X, то F(A) = {f(x) : x ϵ A} называется Образом подмножества А при отображении F. Прообразом подмножества В
X, то F(A) = {f(x) : x ϵ A} называется Образом подмножества А при отображении F. Прообразом подмножества В ![]() Y называется множество {xϵ X:f(x)ϵ B},которое будем обозначать F-1B. В частности, для В = {у} любой элемент из множества F-1B({Y}) называется Прообразому.
Y называется множество {xϵ X:f(x)ϵ B},которое будем обозначать F-1B. В частности, для В = {у} любой элемент из множества F-1B({Y}) называется Прообразому.
Пример. Пусть X = Y = {1,2,3}. Отображение F: X → Y задано следующим образом:
F(1)=1; F(2)=1; F(3)=2.
Тогда F(X) = {1,2}. У элемента 1 ϵ Y два прообраза — 1 и 2; у элемента 2ϵ У один прообраз — 3; у элемента 3 ϵ Y прообразов нет.
Отображение F: X → Y Называется Сюръективным (или Отображением «на»), если F(X) = Y, т. е. для каждого элемента из Y есть прообраз.
Отображение F: X→ Y Называется Инъективным (или Отображением «в»), Если из F(x) = f(x1) следует, что Х = X1, т. е. для каждого элемента Y имеется не более одного прообраза.
Отображение F: X → Y Называется Биективным (или Взаимно-однозначным), если это отображение одновременно и сюръективно, и инъективно, т. е. это отображение «на» и каждый элемент множества Y имеет ровно один прообраз. (Одно и то же правило соответствия может быть сюръективным, инъективным или биективным отображением в зависимости от исходных множеств X и У.)
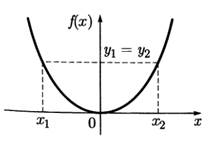
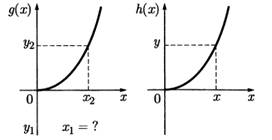
Пример. Обозначим через R+ = {х ϵ R: х ≥ 0}. Рассмотрим следующие три отображения:
F: R→R+ ;g: R+ →R; h: R+ →R+ ;
Эти отображения зададим одной формулой: f(x) = x2; g(x) =x2; h(x) = x2. Они различны, так как различны исходные множества. При этом F является сюръективным, но не инъективным; G — инъективно, но не сюръективно; H — биективно.
Отображения вида F: X→X Называются Преобразованиями множества X.
Тождественным преобразованием данного множества X называется преобразование Ех такое, что Ех (х) = х, ![]() Х ϵ X.
Х ϵ X.
Пусть F: X → Y и G: Y → Z – некоторые отображения. Суперпозицией этих отображений называется отображение Gf: X → Z, определяемое следующим образом:
(gf)(x) = g(f(x)), x ϵX.
Заметим, что суперпозиция определена не для любых пар отображений. Однако суперпозиция двух преобразований одного и того же множества определена всегда.
Пусть F: X → Y и G: Y →Х
Отображение G называется Обратным к отображению F (а отображение F обратным к G), если Fg = еу;gf = ех.
Если обратное отображение существует, то оно единственно. В самом деле, пусть F: X → Y — некоторое отображение множества X во множество Y и отображения G: Y → X и H: Y → X — отображения, обратные к F.
Тогда
(G(Fh))(Y) = (GЕу)(у) = G(у)
И ((Gf)H)(Y) = (ехH)(Y) = H(Y).
Имеем G(Fh) = (Gf)H. Отсюда получаем G(у) = H(Y),![]() YϵY, т. е. отображения g и HСовпадают.
YϵY, т. е. отображения g и HСовпадают.
Обратное отображение обозначается F -1. Оно существует не всегда. Необходимое и достаточное условие существования обратного отображения дает следующая теорема.
Теорема. Отображение F имеет обратное тогда и только тогда, когда оно биективно.
Доказательство. Пусть F: X → Y.
1. Необходимость: Итак, пусть существует обратное отображение F -1 = G: Y → X.
Рассмотрим любой У ϵ Y и Х = G(у). Тогда F(x) = f(g(y)) = у и Х – прообраз У при отображении F. Таким образом, любой У ϵ Y Имеет прообраз X, т. е. F Сюръективно.
Далее, если X, х1ϵ X, причем F(x) = F(Х1), то G(f(x)) = g(f(х1)). Следовательно, т. е.
Ех(X)=ех(х1),
Х = х1 и F инъективно. Отсюда F Биективно, и необходимость доказана.
2. Достаточность: Пусть F Биективно.
Определим отображение G: Y →Х следующим образом. Положим G(у) = х, если F(x) = у. В силу биективности F Отображение G определено на всем Y, и G = F -1.
| < Предыдущая | Следующая > |
|---|