05. Задача линейного программирования (ЗЛП)

Общей задачей линейного программирования (ОЗЛП) называется следующая задача:

(2.1)

, (2.2)

, (2.3)

, (2.4)

, (2.5)

Где – заданные действительные числа, (2.1) –целевая функция, (2.2)-(2.5) – ограничения.

Вектор , координаты которого удовлетворяют ограничениям, называется Допустимым решением задачи.

Множество допустимых решений задачи называют Областью допустимых решений.

Допустимое решение, на котором целевая функция достигает своего максимума (минимума), называется Оптимальным решением или Оптимальным Планом задачи ЛП.

Составим экономико-математические модели некоторых задач линейного программирования.

Пример 1

Имеются стержни длиной 5 м. Необходимо их разрезать на заготовки 2-х видов: А – длиной 1,5 м; В – длиной 0,8 м для производства 20 изделий. На каждое изделие требуется две длинных заготовки (А) и три коротких (В). Определить число стержней, которое необходимо разрезать каждым из возможных способов, чтобы изготовить нужное число изделий и минимизировать отходы.

Решение

Прежде всего, перебрав все возможные способы, построим карту раскроя одного стержня (таблица 1).

Таблица 1

Для изготовления 20 изделий потребуется 40 заготовок А (20´2=40) и 60 заготовок В (20´3=60).

1 Введем переменные. Обозначим за – количество стержней, которые будут разрезаны I способом, – II способом, – III способом, – IV способом.

2 Целевая функция Z – отходы. Ее будем минимизировать. Найдем отходы, полученные при разрезании стержней:

– отходы, полученные при разрезании стержней 1-м способом, так как 5 - 3·1,5 = 0,5;

– отходы, полученные при разрезании стержней 2-м способом, так как 5 - 2·1,5 - 2· 0,8 = 0,4;

– отходы, полученные при разрезании стержней 3-м способом, так как 5 - 1·1,5 - 4· 0,8 = 0,3;

– отходы, полученные при разрезании стержней 4-м способом, так как 5 - 6 0,8 = 0,2.

Тогда .

3 Составим систему ограничений задачи.

1 Ограничение на заготовки А.

При разрезании стержней 1-м способом получим заготовок А, стержней 2-м способом – заготовок А, стержней 3-м способом – заготовок А, при разрезании стержней 4-м способом заготовок А не образуется. Таким образом, всего получим ++ заготовок А, что по условию задачи должно быть не менее 40, т. е. ++.

2 Аналогично получим ограничение на заготовки В:

.

3 Составим ограничения на смысл переменных. Так как количество стержней может быть только неотрицательным числом, то и – целые.

Итак, экономико-математическая модель данной задачи имеет вид

;

Пример 2

Предприятие за 10 часов должно произвести 31 единицу продукции вида Р1 и 36 единиц продукции вида Р2. Для производства продукции каждого вида может быть использовано оборудование А1 или А2.

Производительность оборудования этих групп различна и определяется величиной ед./ч, а стоимость 1 часа работы оборудования составляет  усл. ден. ед./ч , где I – индекс, отличающий вид оборудования, а J – вид продукции. Требуется определить оптимальный план работы групп оборудования, на протяжении 10 часов, при котором будет выполнен план выпуска продукции с минимальной себестоимостью.

, , , ,

, , , .

Решение

Для наглядности составим таблицу 2.

Таблица 2

1 Обозначим за – время работы оборудования по выпуску продукции .

2 Целевая функция будет представлять собой затраты на выпуск продукции, которые необходимо минимизировать. Так как затраты по выпуску продукции на оборудование Составляют , то целевая функция будет иметь вид

,

Т. е. .

3 Составим систему ограничений.

1 Ограничение на выпуск продукции Р1.

На оборудовании А1 будет произведено единиц продукции Р1.

На оборудовании А2 будет произведено единиц продукции Р1.

Таким образом, всего продукции будет произведено , что по условию должно быть равно 31, получим ограничение

, т. е. .

2 Аналогично получим ограничение по выпуску продукции Р2

, т. е. .

3 Ограничение на время работы оборудования А1.

Время работы оборудования А1 по выпуску обоих видов продукции не превышает плановый период 10 ч, следовательно, ограничение будет иметь вид

.

4 Аналогично получим ограничение на время работы оборудования А2

.

5 Введем ограничения на смысл переменных, так как время не может быть отрицательным, то

.

Таким образом, экономико-математическая модель данной задачи будет иметь вид

;

Пример 3

Предприятие может выпускать продукцию двух видов: П1 и П2. Используется три вида ресурсов: оборудование, сырье и электроэнергия. Нормы расхода, запасы ресурсов и прибыль от реализации единицы продукции представлены в таблице 3.

Таблица 3

Найти оптимальный план выпуска продукции.

Решение

Введем переменные:

, – объем выпускаемой продукции П1 и П2 соответственно.

Z – прибыль от реализации всей выпущенной продукции.

Экономико-математическая модель данной задачи будет иметь вид

;

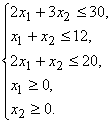
Методы решения задач линейного программирования будут рассмотрены ниже.

Формы записи задач линейного программирования

Симметричной (стандартной) формой записи ЗЛП называется задача максимизации целевой функции (2.1) при ограничениях вида (2.2) и (2.5) Или задача минимизации целевой функции (2.1) при ограничениях вида (2.4) и (2.5), т. е.

;

,

Или ;

,

,

Где – заданные действительные числа.

Канонической формой записи ЗЛП называется задача минимизации или максимизации целевой функции (2.1) при ограничениях вида (2.3) и (2.5), т. е.