1.1.4. Произведение матриц
Умножение матрицы А = ||Aij|| размера ![]() на матрицу В = ||Bij|| размера
на матрицу В = ||Bij|| размера ![]() определено лишь для случая, когда число столбцов матрицы А совпадает с числом строк матрицы В, т. е. когда N=L. В этом случае произведение матриц определяется следующим образом:
определено лишь для случая, когда число столбцов матрицы А совпадает с числом строк матрицы В, т. е. когда N=L. В этом случае произведение матриц определяется следующим образом:
|
Произведением матриц АВ называется матрица С = ||СIj|| размера
|
Иначе говоря, элемент Cij равен сумме произведений элементов I-ой строки матрицы А на соответствующий элемент J-ого столбца матрицы В. С помощью знака суммирования можно записать это так:

Пример 2.
Найти произведение матриц
 и
и  .
.
Имеем
 .
.
Отметим, что произведение матриц некоммутативно, т. е. в общем случае АВ Не равно ВА. В приведённом выше примере матрицу В просто нельзя даже умножить на матрицу А. Но, даже если А и В – квадратные матрицы одного порядка (тогда существуют произведения АВ и ВА), то, как показывает следующий пример, произведения АВ и ВА могут не совпадать.
Пример 3.
Пусть  ,
,  .
.
Тогда  ,
,
 .
.
Единичной матрицей называется квадратная матрица вида
 .
.
Упражнение 5.
Доказать, что для любой квадратной матрицы А
АЕ=ЕА=А,
Где Е – единичная матрица того же порядка, что и А.
Доказательство.
Пусть А и Е – квадратные матрицы П-го порядка, В = АЕ.
Тогда Bij = Ai1E1J + Ai2E2J + ... + Aijejj + ... + Ainenj.
Но Eij = 0 при I, не равном J, a Ejj = 1. Следовательно, Bij = Aij·1 = Aij. Таким образом, все элементы матрицы В равны соответствующим элементам матрицы А, то есть В = А.
Если матрица С = ЕА, то СIj = еI1А1J + еI2А2J + ... + ЕIiАIj + ... + ЕInАNj = 1·Aij = Aij
(учитываем, что Eii = 1, Eij = 0 при I, не равном J). Значит, С = А. Утверждение доказано.
Приведём ряд свойств произведений матриц.
|
1. (АВ)С=А(ВС) |
Доказательство.
Пусть размер матрицы A = ||Aij|| ![]() матрицы B = ||Bij|| -
матрицы B = ||Bij|| - ![]() а матрицы
а матрицы
C = ||Cij|| ![]() Имеем AB = ||AIj||, где
Имеем AB = ||AIj||, где

Тогда (AB)C = ||GIj||, где

Где 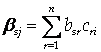 - элемент матрицы ВС. Тем самым, если обозначить элемент матрицы А(ВС) через G’Ij, будем иметь
- элемент матрицы ВС. Тем самым, если обозначить элемент матрицы А(ВС) через G’Ij, будем иметь

|
2. А(В+С)=АВ+АС, (В+С)А=ВА+СА |
Доказательство.
Пусть матрица A = ||Aij|| имеет размер ![]() а матрицы B = ||Bij|| и C = ||Cij|| имеют размер
а матрицы B = ||Bij|| и C = ||Cij|| имеют размер ![]() Тогда для элементов матрицы А(В+С)= ||GIj|| имеем
Тогда для элементов матрицы А(В+С)= ||GIj|| имеем

Из определения произведения матриц вытекает, что АВ= ||AIj||, а АС= ||BIj||, т. е. А(В+С)=АВ+АС. Аналогично доказываем, что (В+С)А=ВА+СА.
Упражнение 1.6.
Пусть А и В – квадратные матрицы одного порядка. Вывести формулу для (А+В)2 (при натуральном П Под СN Понимается произведение С·С·…·С).
Используем свойства сложения и умножения матриц:
(А + В)2 = (А + В)(А + В) = (А + В)А + (А + В)В = А·А + В·А + А·В +В·В =
= А2 + В·А + А·В +В2.
|
Заметьте, что результат может совпасть с Формулой сокращенного умножения (А + В)2 = А2 + 2АВ + В2 Только в том случае, если АВ = ВА. В общем случае это неверно!
|
Ответ: (А + В)2 = А2 + В·А + А·В +В2.
Упражнение7.
Пусть А и В – квадратные матрицы одного порядка. Разложить на множители выражение АВ+2В.
Используем свойство единичной матрицы (см. упражнение 5):
|
АЕ = ЕА = А. |
Следовательно, В = ЕВ. Тогда АВ + 2В = АВ + (2Е)В = (А + 2Е)В
(использовано свойство 2 произведения матриц).
Ответ: АВ + 2В = (А + 2Е)В.
Упражнение 8.
Пусть А,В и С – квадратные матрицы одного порядка. Разложить на множители выражение А2С +АС 2.
Решение.
Поскольку А2 = А·А, С2 = С·С, запишем заданный матричный многочлен в виде: А2С +АС 2 = А·А·С +А·С·С и воспользуемся свойствами произведения матриц:
А·А·С +А·С·С = А(А·С +С·С) = А((А + С)С) = А(А + С)С.
Ответ: А2С +АС 2 = А(А + С)С.
Упражнение 9.

Найти АВ и ВА.
Решение.
Определим размеры матрицы А: ![]() и В:
и В: ![]() Следовательно, существуют оба произведения: и АВ, и ВА, причем размер матрицы С = АВ:
Следовательно, существуют оба произведения: и АВ, и ВА, причем размер матрицы С = АВ: ![]() а матрицы D = BA:
а матрицы D = BA: ![]()
Вычислим элементы матрицы С:

Таким образом, матрица С имеет вид:
 .
.
Матрица D состоит из единственного элемента:
![]()
Тогда ![]() .
.
Ответ:  ,
, ![]() .
.
| < Предыдущая | Следующая > |
|---|