7.1.2. Транспортная задача

Это задача о наиболее экономном плане перевозок однородного или взаимозаменяемого продукта из пунктов производства (станций отправления) в пункты потребления (станции назначения).

Транспортная задача является важнейшей частной моделью линейного программирования, имеющей обширные практические приложения не только к проблемам транспорта. Особо важное значение она имеет в деле рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта.

7.1.2.1. Постановка задачи и ее математическая модель

Некоторый однородный продукт производится в m пунктах производства A1, A2, ..., Am. Задан объем производства at пункта Ai (i = I, m). Произведенный продукт должен быть перевезен в п пунктов потребления B1, B2, ..., Bn. Известен спрос bj пункта Bj (j = I, n). Заданы также транспортные издержки Cj-, связанные с перевозкой единицы продукта из пункта Ai в пункт Bj. Требуется составить план перевозок, обеспечивающий при минимальных транспортных расходах (издержках) удовлетворения спроса всех пунктов потребления за счет продукта, произведенного во всех пунктах производства.

Обозначим через Xij количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю. Тогда условие задачи можно записать в виде табл. 7.5, которую в дальнейшем будем называть матрицей планирования.

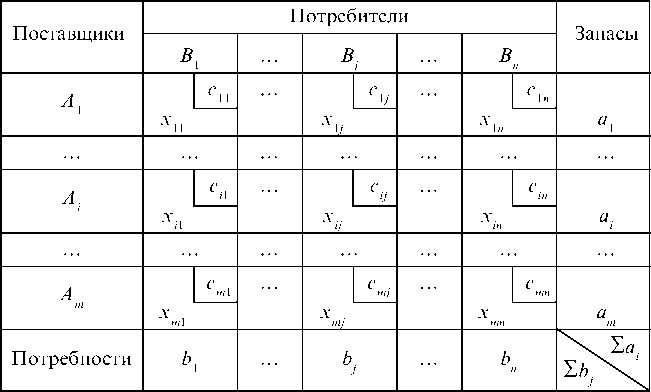
Поэтому математическая формулировка транспортной задачи сводится к минимизации линейной формы

при ограничениях

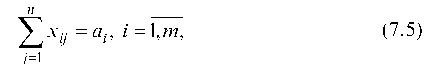
(ограничения по запасам),

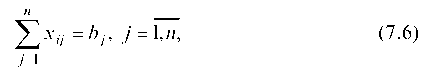
(ограничения по потребностям),

Различают задачи с закрытой моделью, когда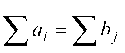И

открытой моделью, когда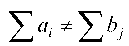, т. е. баланс между запаса

ми и потребностями отсутствует.

376

Необходимым и достаточным условием разрешимости транспортной задачи является равенство суммарных запасов суммарным потребностям, т. е.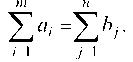

Если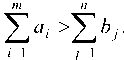, то вводят фиктивный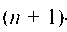-й пункт назна

чения с потребностью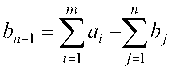И полагают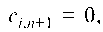

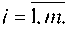
Если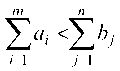, то вводят фиктивный (m + 1)-й пункт

отправления с запасами груза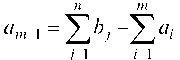И принимают

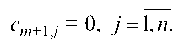
Математическая модель транспортной задачи относится к задачам линейного программирования и может быть решена симплексным методом. Однако ввиду исключительной практической важности этой задачи и специфики ограничений (7.5) — (7.7): ограничения заданы в виде уравнений; каждая неизвестная входит лишь в два уравнения, коэффициенты при неизвестных — единицы, для ее решения созданы специальные алгоритмы. Самым распространенным методом решения транспортной задачи является метод потенциалов.

Решение транспортной задачи разбивается на два этапа:

1. Определение начального допустимого базисного решения (первого опорного плана) — первоначальное распределение поставок.

2. Построение последовательных итераций (шагов), улучшающих опорные планы (каждый новый план не должен увеличивать суммарные затраты).

После выполнения первого этапа шаги второго этапа проводятся до тех пор, пока не будет найдено оптимальное распределение поставок.

7.1.2.2. Построение первоначального опорного плана

Рассмотрим два метода построения первого опорного плана.

План составляется последовательным заполнением по одной клетке в таблице перевозок так, что каждый раз либо полностью удовлетворяется потребность одного из потребителей, либо полностью ввозится груз от некоторого поставщика. В теории дока-

зывается, что базисное решение системы ограничений (из m + n уравнений с mn переменными) в условиях транспортной задачи имеет m + n - 1 базисных переменных (ее ранг равен m + n - 1), поэтому, совершив m + n - 1 указанных шагов, получим первый опорный план. Различие двух методов отыскания первого опорного плана состоит в различии способов выбора последовательности заполнения клеток.

Диагональный метод или метод северо-западного угла. При этом методе на каждом шаге построения первого опорного плана заполняется верхняя левая клетка («северо-западный угол») оставшейся части таблицы. При таком методе заполнение таблицы начинается с клетки переменного Xn и заканчивается в клетке неизвестного Xmn, т. е. идет как бы по диагонали таблицы перевозок.

Метод наименьшей стоимости. Исходное опорное решение, построенное диагональным методом, как правило, оказывается весьма далеким от оптимального, так как при его определении совершенно игнорируются величины затрат с.. Поэтому требуются в дальнейших расчетах много итераций для достижения оптимального плана. Число итераций можно сократить, если исходный план строить по более рациональному правилу «минимального элемента». Сущность его состоит в том, что на каждом шаге заполняется клетка с наименьшей величиной с.. Если такая клет-

1J

ка не единственная, то лучше заполнять ту, по вертикали или горизонтали которой встречаются большие с., а в принципе заполняется любая из них.

Пусть это будет клетка (i, j). Запишем в эту клетку х. = min (a, b). Если ai < bj, то запасы поставщика Ai исчерпаны, а потребность В. стала b' = b. - at. Поэтому, не принимая более во внимание i-ю строку, снова ищем клетку с наименьшей стоимостью перевозок и заполняем ее с учетом изменившихся потребностей. Для случая аг - > b. из рассмотрения исключаетсяу-й столбец, а запасы Ai полагаются равными а' = аг - - b.. Продолжаем этот процесс до тех пор, пока все запасы не будут исчерпаны, а все потребности — удовлетворены. Необходимо отметить, что при наличии в таблице клеток с одинаковыми тарифами, планы, полученные с помощью этого метода, могут быть разными, однако они, несомненно, ближе к оптимальному, чем план, составленный по методу северозападного угла.

Прежде чем перейти к анализу оптимальности планов и способам их улучшения, выясним, каким требованиям должны удовлетворять составляемые планы. Для этого вернемся к системе ограничений (7.5) — (7.7). Очевидно, что первая группа уравнений требует, чтобы сумма элементов плана по i-й строке равнялась at,

i = 1, m; а вторая группа — чтобы сумма элементов по j-му столбцу была равна bj> j = 1, п. Условие закрытости модели транспортной задачи означает, что среди m + п уравнений системы ограничений независимых только m + п - 1, поэтому в любом базисном решении этой системы должно быть m + п - 1 базисных переменных. Поскольку свободные переменные в таком решении равны нулю, то в транспортной таблице им будут соответствовать пустые клети.

Клетки таблицы, в которых записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.

В теории доказано, что базисное решение системы ограничений (7.5) — (7.7) в условиях транспортной задачи должно иметь m + п - 1 базисных переменных.

План называется вырожденным, если количество базисных клеток в нем меньше, чем m + п - 1.

Если на каком-то этапе решения получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток 0 и тем самым объявив их базисными. Поскольку этим дополнительным клеткам будут отвечать нулевые перевозки, то общий баланс и суммарная стоимость перевозок плана при этом не изменится. Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. Приведем условия, которым должен соответствовать пополненный план.

Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ломаная может иметь точки самопересечения, но не в клетках цикла.

План называется ациклическим, если его базисные клетки не содержат циклов.

Доказано, что оптимальные планы являются ациклическими, поэтому и первоначальный план также должен удовлетворять этому требованию. Заметим, что планы, полученные с помощью ме-

тодов северо-западного угла и наименьшей стоимости, ациклические. Однако если план оказался вырожденным, то при его пополнении требование ацикличности необходимо учитывать.

7.1.2.3. Оптимальность базисного решения.

Метод потенциалов

Получив первый опорный план, следует проверить его оптимальность и, если требуется, перейти к новому опорному плану с лучшим значением целевой функции Z. Для этого применяют метод потенциалов. Каждому поставщику Ai и каждому потребителю Bj сопоставляют, соответственно, величины Ui и Vj — потенциалы этих пунктов.

Для того чтобы некоторый опорный план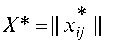Транс

портной задачи был оптимальным, необходимо и достаточно,

чтобы ему соответствовала система из (m + п) чисел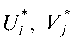, удов

летворяющих условиям:

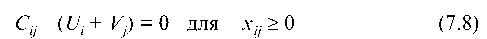
(для занятых клеток) и

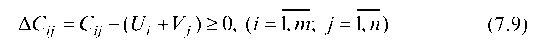
(для свободных клеток).

Числа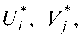Называются потенциалами соответственно про

изводителей и потребителей, вся их система — потенциальной, а условия (7.8) — (7.9) — условиями потенциальности системы

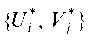; каждое в отдельности неравенство (равенство) называется условием потенциальности для соответствующей клетки (i, j).

Поскольку число неизвестных потенциалов (m + п) всегда на единицу больше числа уравнений (числа заполненных клеток) N = m + п - 1, то выбираем строку, где есть занятая клетка и для этой строки назначаем потенциал равным нулю, например U1 = 0, и легко находим последовательно из уравнений (7.8) значения остальных потенциалов.

Если же число заполненных клеток N < m + п - 1, то вводим дополнительно необходимое количество занятых клеток с нуле-

выми перевозками Xij = 0, которые нужны для определения потенциалов из уравнений (7.8).

Затем для всех свободных клеток из соотношений (7.9) определяем величину ACjj и, если все DCj > 0, то получим оптимальный план перевозок, если же встречаем отрицательные ACi, то план не оптимален и его надо улучшать.

7.1.2.4. Улучшение плана перевозок

Среди пустых клеток с отрицательными значениями ACj выбираем ту, у которой ACjj наименьшая. Эта пустая клетка рекомендуется к заполнению, в результате которого одна из заполненных клеток станет пустой. Процедура перепланировки соответствует взаимной перемене роли двух переменных в симплексном методе. Например, в табл. 7.5 клеткой, рекомендуемой к заполнению служит пустая клетка (1, 2), следовательно, переменная X12 из не основных (нулевых) переходит в основные (положительные). Остается определить, какая из основных переменных должна стать не основной.

Для свободной клетки строим замкнутую ломанную линию (цикл), состоящую из горизонтальных и вертикальных отрезков прямых. Одна из вершин находится в свободной клетке, а остальные в занятых клетках, число вершин всегда четное. Свободной вершине придаем знак плюс, знаки остальных вершин чередуются. На каждой стороне этой ломанной линии — контура могут находиться две заполненные вершины, кроме того одна вершина лежит в заполняемой пустой клетке.

Наиболее часто контур имеет вид прямоугольника, но возможны фигуры другого типа (рис. 87).

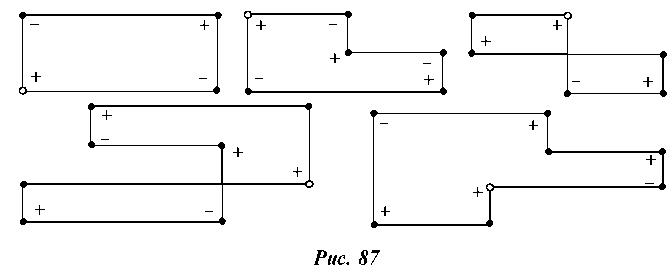
Перепланировке подвергаются только клетки контура, а величина перевозок во всех остальных заполненных клетках таблицы не изменяется.

В отрицательных вершинах контура выбираем наименьшее число и это число прибавляем к положительным вершинам и отнимаем от отрицательных вершин. Выбранная отрицательная вершина станет свободной, число занятых вершин не изменится, баланс перевозок старого и нового контура останется без изменения.

Далее строим новую таблицу перевозок и проверяем оптимальность плана. Если план оптимальный, то получим оптимальное решение транспортной задачи, если нет, то план улучшаем. Через какое-то число последовательных шагов улучшения планов перевозок будет получен оптимальный план.

7.1.2.5. Задача определения оптимального плана перевозок

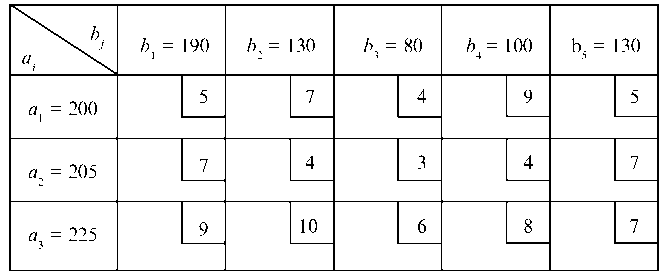
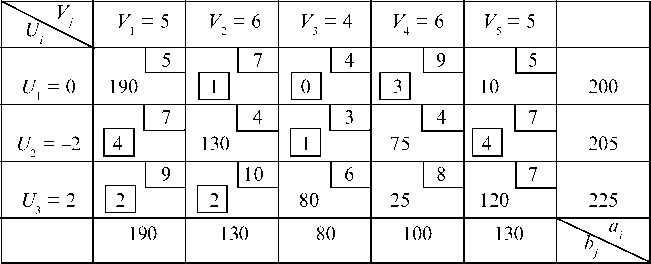
На три базы A1, A2, A3 поступил однородный груз в количестве 200, 205, 225 тонн. Полученный груз требуется перевезти в пять пунктов B1, B2, ..., B5, потребности которых составляют 190, 130, 80, 100 и 130 тонн. Расстояние Cij в ед. км. (i = 1, 2, 3; 7 = 1, 2, ., 5) между пунктами отправления и пунктами назначения приведены в табл. 7.6.

Следует спланировать перевозки однородного груза так, чтобы общие затраты всех перевозок в тонно-километрах были бы минимальными.

Таблица 7.6

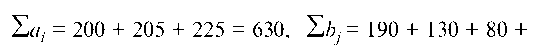
Так как

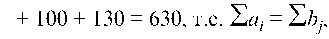То имеем закрытую модель транспортной задачи.

Составляем исходное опорное решение по правилу минимальной стоимости. В клетке (2, 3) наименьшая стоимость C23 = 3 и туда отправляем весь необходимый груз 80 т. Далее наименьшая стоимость С24 = С22 = 4 и в клетку (2, 4) направляем все 100 т необходимого груза, а в клетку (2, 2) — оставшиеся на базе А2 25 т. Теперь наименьшая стоимость Cn = Ci5 = 5 и в клетку (1, 1) направляем 190 т необходимого груза, а в клетку (1, 5) — 10 т оставшегося на базе A1 груза. Затем направляем 120 т груза в клетку (3, 5) и 105 т в клетку (3, 2). Правильность заполнения таблицы проверяем суммируя грузы в заполненных клетках по строкам и столбцам. Получим опорное решение (табл. 7.8).

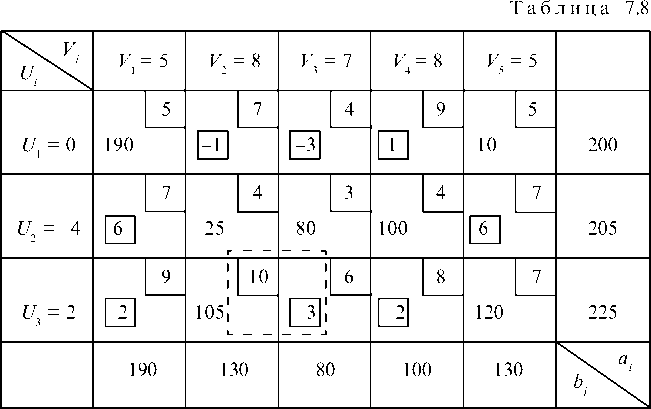
Всего должно быть заполненных клеток N = m + п - 1 = = 3 + 5 - 1 = 7, у нас также заполнено семь клеток.

Проверяем оптимальность полученного плана перевозок методом потенциалов.

Поставщику ставим в соответствие потенциалы Ui (i = 1, 2, 3), а потребителю — Vj (j = 1, 2, ., 5) и определяем их. Назначаем U = 0, а все остальные потенциалы находим из условия, что для занятых клеток должны выполняться условия (7.8):

Для всех свободных клеток находим ACy из соотношения (7.9) и записываем в табл. 7.8 в прямоугольники I I.

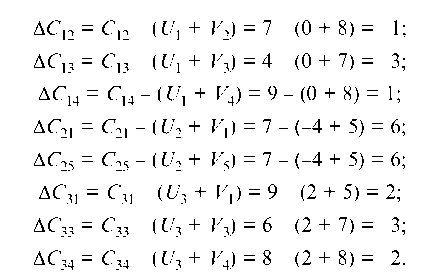
Так как имеются AC,-,- < 0, то, согласно п. 7.1.2.3, план табл. 7.8

1J

не является оптимальным и его нужно улучшить соответственно п. 7.1.2.4.

Для свободной клетки (3; 3) с наименьшим отрицательным C33 = -3 строим контур (пунктирный прямоугольник) и улучшаем соответствующий ему план перевозок.

25

Старый контур

Новый контур

.80

105

+ -	»-о
- + • ^	!>

Среди отрицательных вершин выбираем наименьшее значение 80 и прибавляем его к положительным вершинам и отнимаем от отрицательных вершин. Получили новый контур перевозок опять с одной свободной вершиной и не нарушенным балансом перевозок. Далее строим новый план перевозок (табл. 7.9).

Таблица 7.9

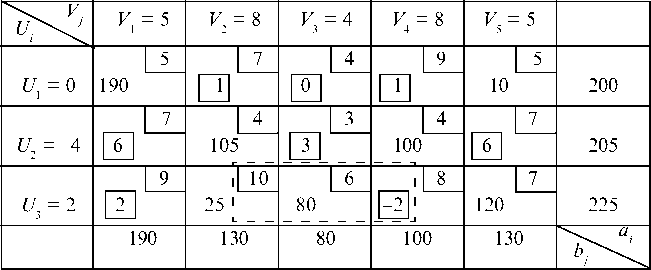
Проверяем его оптимальность, находя потенциалы U, Vj и ДС1

Так как ДС34 = -2 < 0, то для клетки (3, 4) строим улучшенный контур.

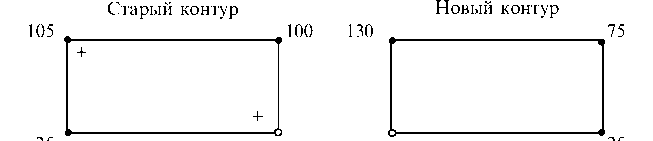
25 25

Строим улучшенный план перевозок (табл. 7.10).

Таблица 7.10

Так как все ДСу > 0, то получен оптимальный план перевозок. X — (х11 — 190, Х]2 — 0, Х13 — 0, Х14 — 0, Х15 — 10,

Х21 — 0 Х22 — 130, Х23 — 0 Х24 — 75, Х25 — 0

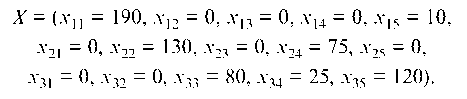
Х31 — 0, Х32 — 0, Х33 — 80, Х34 — 25, Х35 — 120).

Транспортные расходы при этом будут минимальными:

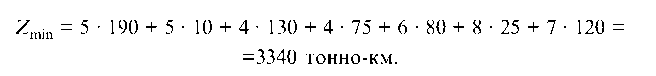
Zmin — 5 • 190 + 5 • 10 + 4 • 130 + 4 • 75 + 6 • 80 + 8 • 25 + 7 • 120 —

—3340 тонно-км.

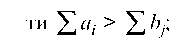
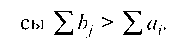
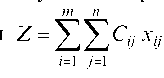
ограничениях

7.1.2.6. Открытая модель транспортной задачи

Для открытой модели может быть два случая:

а) суммарные запасы превышают суммарные потребности S a > S Ь;

б) суммарные потребности превышают суммарные запасы S b > S

Формулироваться данная задача будет следующим образом.

m П

Найти min значение линейной функции Z = ZZCj x, j при

(случай Ь) (7.11)

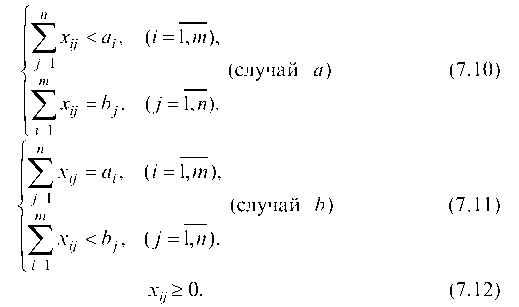
(7.12)

Открытая модель решается приведением к закрытой.

В случае (а) вводится фиктивный потребитель Вп+1, потребности которого Ь„+1 — Е а - Е Ьг 386

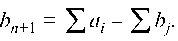
В случае (б) вводится фиктивный поставщик ^т+1, запасы ко-

т°р°го «т+1 — Еь7- - Еа.

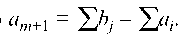
Стоимости перевозок в обеих случаях полагаются равными нулю.

При равных стоимостях перевозки единицы груза от поставщиков к фиктивному потребителю затраты на перевозку груза реальным потребителям минимальны, а фиктивному потребителю будет направлен груз от наименее выгодных поставщиков. Составить оптимальный план перевозок.

Имеем матрицу планирования (табл. 7.11).

Таблица 7.11

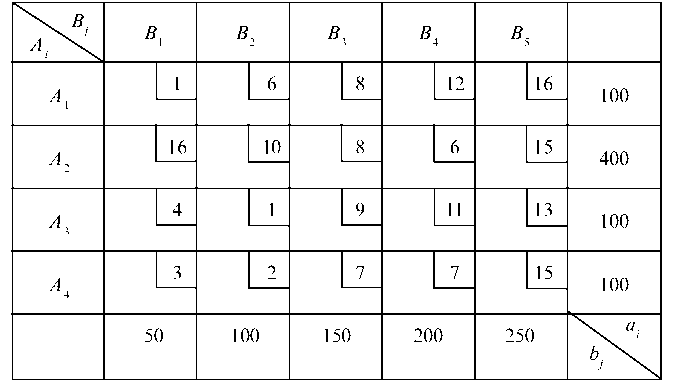
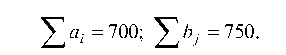
Вводим фиктивного поставщика ^m+1 = A5, объем запасов которого am+1 = а5 = 50. При составлении опорного плана методом min стоимости необходимо наименьшую стоимость выбирать только среди стоимостей реальных поставщиков и потребителей, а запасы фиктивного поставщика распределять в последнюю очередь.

Число заполненных клеток 7, а должно быть m + n - 1 = = 5 + 5 - 1 = 9, тогда в клетках (4, 2) и (3, 5) ставим нули.

Находим U, Vj и ДС^ и записываем их в табл. 7.12 в I—I. Так как все ДСу > 0, то получили оптимальный план перевозок (табл. 7.12).

Найдем суммарную стоимость перевозок по оптимальному плану:

Таблица 7.12

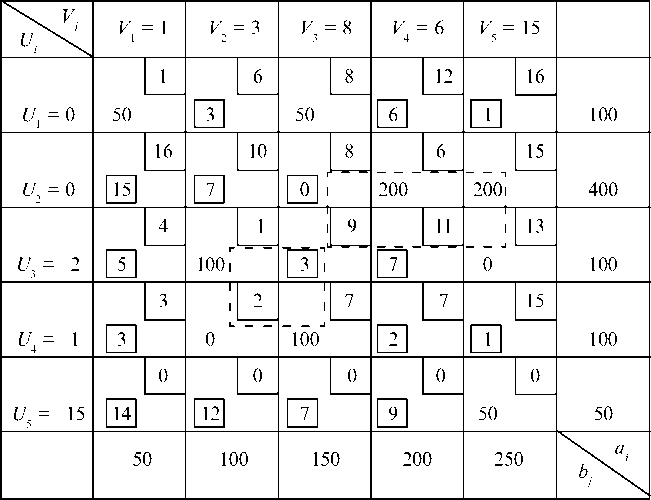
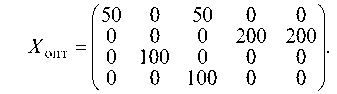
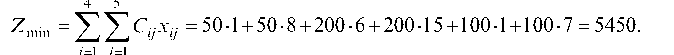
Анализируя этот план, можно сделать следующие выводы. Потребитель В5 получает 50 ед. груза от фиктивного поставщика, следовательно, его потребности будут неудовлетворены на это же количество единиц.

Оптимальный план не является единственным, так как для клетки ^2^3 сумма потенциалов равна стоимости перевозок и в нее по циклу можно переместить 100 ед. груза. При перераспределении система потенциалов не изменится и стоимость перевозок останется прежней.

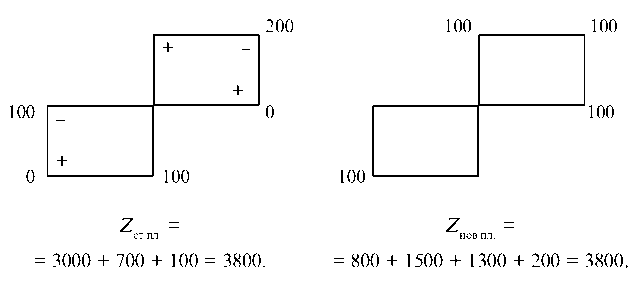
7.2. Математические методы в экономике

< Предыдущая		Следующая >