Контрольная работа по мат. анализу 25

В штате гаража числится 54 водителя. Сколько свободных дней может иметь каждый водитель в месяц (30 дней), если ежедневно 25% автомашин из имеющихся 60 остаются в гараже для профилактического ремонта.

Решение:

	Машин ежедневно остается в гараже на профилактическом ремонте.
	Машин с водителями ежедневно уходят в рейс.
	Водителей из штата гаража ежедневно не выходит в рейс из-за профилактического ремонта автомашин.
	Количество водителей в течение месяца, не выходящих в рейс из-за профилактического ремонта автомашин.
	Дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин.

Ответ:

Каждый водитель из штата гаража в течение месяца может иметь свободных дней.

Задание №3. Вопрос №1.

Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если , .

Решение:

Построим в плоскости POQ график функции спроса Q=QD(P) и предложения Q=QS(P). Для этого найдем координаты пересечения с осями координат:

С осью OP (Q=0):

С осью OQ (P=0):

Для Q=QS(P):

Для Q=QD(P):

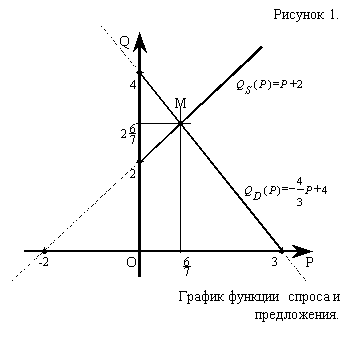
подпись: рисунок 1.

график функции спроса и предложения.

Т. к. функции QS(P) и QD(P) – линейные функции, то их графиками являются прямые, для построения которых достаточно определить их точки пересечения с осями координат. Они найдены, значит можно производить построение графика (рис.1).

Найдем точку равновесия графиков функции спроса и предложения (М), в которой спрос равен предложению. Для этого решим систему:

, из этой системы получаем:

, тогда , значит координаты т. M.

Ответ:

Координаты точки равновесия равны ,

Задание №12. Вопрос №9.

Используя правила вычисления производных и таблицу, найдите производные следующих функций:

Решение:

Ответ:

Производная заданной функции равна

Задание №13. Вопрос №2.

Используя дифференциал функции, найдите приближенное значение

Числа:

Решение:

Ответ:

Приближенное значение заданного числа равно 1,975.

Задание №18. Вопрос №9

Исследуйте функцию и постройте ее график:

Решение:

Область определения данной функции: .

Найдем точки пересечения с осями координат:

С осью OY :

С осью OX :

, дробь равна нулю, если ее числитель равен нулю, т. е.

Точка пересечения:

Точки пересечения: ,

Т. к. все точки входят в область значений функции, то точек разрыва НЕТ.

Вертикальных асимптот у графика функции нет, т. к. нет точек разрыва. Правая и левая наклонные асимптоты имеют уравнение: , где:

Т. к. правая и левая наклонные асимптоты совпадают, то уравнение имеет вид: , т. е. - уравнение горизонтальной асимптоты.

Найдем точки экстремума заданной функции. Для этого найдем ее первую производную:

Т. к. если у функции есть точка экстремума, то в этой точке первая производная функции равна нулю, т. е. :

, дробь равна нулю, если ее числитель равен нулю, т. е. , отсюда , следовательно , значит точка - точка экстремума функции.

подпись: рисунок 2.

исследование на экстремум.

На участке производная > 0, значит, при , заданная функция возрастает.

На участке производная < 0, значит, при , заданная функция убывает (рис 2.).

Следовательно - точка максимума заданной функции .

Найдем участки выпуклости/вогнутости заданной функции. Для этого найдем ее вторую производную:

Т. к. если у функции есть точка перегиба, то в этой точке вторая производная функции равна нулю, т. е. :

, дробь равна нулю, если ее числитель равен нулю, т. е. , значит , тогда , отсюда

Отсюда , .

подпись: рисунок 3.

исследование на выпуклость. На участке производная >0, значит это участок вогнутости графика функции.

На участке производная >0,

Значит это тоже участок вогнутости графика функции.

Следовательно, при график заданной функции является вогнутым.

На участке производная <0, значит, при график заданной функции является выпуклым (рис. 3).

Следовательно, точки , - точки перегиба графика заданной функции .

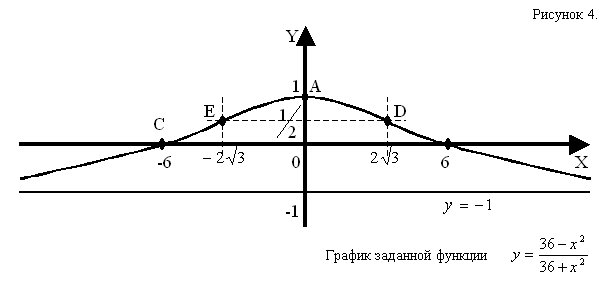
подпись: рисунок 4.

график заданной функции
Выполненные исследования заданной функции позволяют построить ее график (см. рис. 4).

Часть II.

Задание №8. Вопрос №8.

Фирма производит товар двух видов в количествах и. Задана функция полных издержек . Цены этих товаров на рынке равны и . Определить, при каких объемах выпуска достигается максимальная прибыль, найти эту прибыль.

, ,

Решение:

Пусть - функция прибыли, тогда

Найдем первые частные производные функции :

, . Найдем стационарные точки графика функции . Для этого решим систему:

Следовательно - стационарная точка. Проверим ее на экстремум, для этого

Введем обозначения: , , ,

Тогда , , , . Т. к. > 0, то экстремум есть, а т. к. < 0, то это максимум. Следовательно, при объемах выпуска И , достигается максимальная прибыль равная:

Ответ:

и достигается при объемах выпуска И .

Задание №12. Вопрос №9.

Вычислить неопределенный интеграл:

Решение:

Ответ:

Задание №14. Вопрос №2.

Вычислить несобственный интеграл (или установить его расходимость) .

Решение:

Ответ:

Данный несобственный интеграл – расходящийся.

Задание №15. Вопрос №6.

Решить уравнение

Решение:

. Разделив обе части на , получим . Проинтегрируем полученное уравнение . Представим , как , тогда

Ответ:

Решением данного уравнения является .

Задание №18. Вопрос №9.

Найти общее решение уравнения:

Решение:

Найдем корни характеристического уравнения: , тогда , следовательно , , тогда

Фундаментальную систему решений образуют функции:

Т. к. действительные и мнимые решения в отдельности являются решениями уравнения, то в качестве линейно независимых частей решений и , возьмем , , тогда общее решение однородного уравнения будет иметь вид:

Представим правую часть уравнения, как и сравним с выражением, задающим правую часть специального вида:

. Имеем , , тогда т. к. - многочлен второй степени, то общий вид правой части: . Найдем частные решения:

, ,

Сравним коэффициенты при слева и справа, найдем , решив систему:

, отсюда .

Тогда общее решение заданного неоднородного линейного уравнения имеет вид: .

Ответ:

Дополнительно

Часть I.

Задание №7. Вопрос №1.

Найти предел: .

Решение:

Ответ:

Заданный предел равен .

Задание №9. Вопрос №8.

Найдите уравнение асимптот и постройте их графики:

Решение:

Область определения данной функции: .

Т. к. точка не входят в область значений функции, то это точка разрыва, а т. к. и , следовательно, уравнение – уравнение вертикальной асимптоты.

Уравнения правой и левой наклонных асимптот имеют вид: , где:

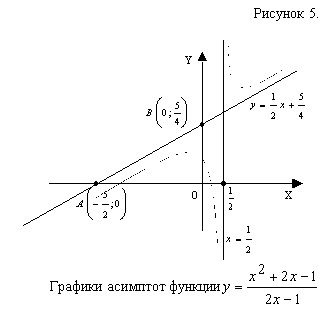подпись: рисунок 5.

графики асимптот функции Т. к. правая и левая наклонные асимптоты совпадают, то уравнение наклонной

Асимптоты имеет вид: .

Для построения графиков асимптот (см. рис. 5), найдем

Точки пересечения наклонной асимптоты с осями

координат:

С осью OX: точка,

С осью OY: точка

Ответ:

и – уравнения асимптот заданной функции.

Задание №11. Вопрос №6.

Исходя из определения производной, докажите: .

Решение:

Т. к. по определению производная функции в точке вычисляется по формуле , тогда приращение в точке : .

Следовательно .

Ответ:

Задание №15. Вопрос №1.

Найдите пределы, используя правило Лопиталя: .

Решение:

Ответ:

Заданный предел равен .

Дополнительно. Часть II.

Задание №7. Вопрос №1.

Написать в точке уравнение касательной плоскости к поверхности, заданной уравнением: .

Решение:

Уравнение касательной плоскости к графику функции в точке имеет вид: . Поэтому, продифференцируем заданное уравнение поверхности: . Подставив в полученное уравнение координаты точки вместо значений переменных, и заменив дифференциалы переменных на их приращения, получим:

Ответ:

Уравнение касательной плоскости к заданной поверхности в заданной точке имеет вид .

Задание №9. Вопрос №8.

Найти наибольшее и наименьшее значение функции в области: .

Решение:

Т. к. заданная функция дифференцируется в замкнутой ограниченной области, то свое наибольшее/наименьшее значение она достигает или в стационарной точке внутри области дифференцирования, или на границе области.

Найдем стационарные точки заданной функции, для этого решим систему:

, точка не принадлежит заданной области дифференцирования, значит стационарных точек внутри области нет, следовательно, наибольшее/наименьшее значение функцией достигается на границе области дифференцирования. Граница области ограничена окружностями и . Найдем наибольшее/наименьшее значение на границах области дифференцирования. Для этого составим функцию Лагранжа:

, тогда , , следовательно, система уравнений для определения координат экстремальной точки имеет вид:

Эта система имеет четыре решения:

, ,	Точка – точка условного максимума, при этом функция .
, ,	Точка – точка условного максимума, при этом функция .
, ,	Точка – точка условного минимума, при этом функция .
, ,	Точка – точка условного минимума, при этом функция .

, тогда , ,

Следовательно, система уравнений для определения координат экстремальной точки имеет вид:

Эта система также имеет четыре решения:

, ,	Точка – точка условного максимума, при этом функция .
, ,	Точка – точка условного максимума, при этом функция .
, ,	Точка – точка условного минимума, при этом функция .
, ,	В точке – точка условного минимума, при этом функция .

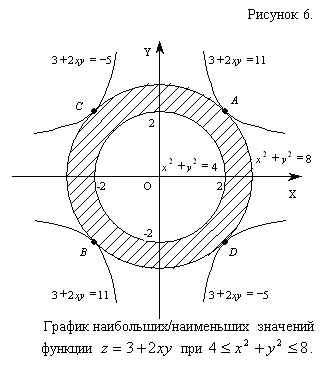
подпись: рисунок 6.

график наибольших/наименьших значений функции при .

Следовательно, заданная функция в заданной области дифференцирования достигает наибольшего значения в точках и и наименьшего в точках и при этом графики функций и касаются окружности в точках , и , соответственно (см. рис.6).