Контрольная работа по мат. анализу 18
Контрольная работа №1
Задания 1-10. При условном делении экономики на три отрасли задана матрица коэффициентов прямых затрат А и вектор конечной продукции Y. Требуется:
1. Записать уравнение линейного межотраслевого баланса в координатной форме.
2. Найти плановые объемы выпуска валовой продукции отраслей. Систему линейных алгебраических уравнений решить методом Гаусса. Решение системы записать в неправильных дробях.
3. Выполнить проверку результата.
4. Записать приближенный ответ с точностью до сотых.
А =  , Y =
, Y = ![]()
1. Уравнение линейного межотраслевого баланса имеет вид ![]() , где
, где  Вектор валового выпуска продукции,
Вектор валового выпуска продукции,  Вектор конечного потребления,
Вектор конечного потребления, ![]() Матрица прямых материальных затрат. Известны вектор конечного потребления
Матрица прямых материальных затрат. Известны вектор конечного потребления 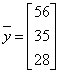 и матрица прямых материальных затрат
и матрица прямых материальных затрат  .
.
Подставим в уравнение Леонтьева ![]() векторы
векторы ![]() и матрицу А:
и матрицу А:
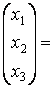

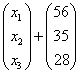 .
.
Используя правила умножения матриц, сложения векторов и определение равенства векторов, получаем систему уравнений:
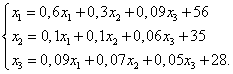
Полученная система – это векторное уравнение линейного межотраслевого баланса в координатной форме.
Для решения этой системы приведем подобные члены:
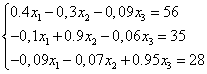
Все уравнения умножим на 100:
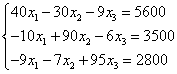
2. Решим полученную систему методом Гаусса.
Метод Гаусса.
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Умножим 1-ую строку на (10). Умножим 2-ую строку на (-9). Добавим 2-ую строку к 1-ой:
Умножим 2-ую строку на (4). Добавим 3-ую строку к 2-ой:
Для удобства вычислений поменяем строки местами:
Умножим 1-ую строку на (880). Умножим 2-ую строку на (330). Добавим 2-ую строку к 1-ой:
Из 1-ой строки выражаем x3 ![]()
Из 2-ой строки выражаем x2 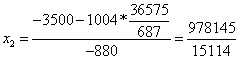
Из 3-ой строки выражаем x1 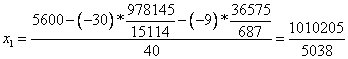
Итак, решение системы в неправильных дробях будет иметь вид: ![]() ,
, ![]() ,
, ![]() . Они будут выражать плановые объемы выпуска валовой продукции отраслей.
. Они будут выражать плановые объемы выпуска валовой продукции отраслей.
3. Выполним проверку полученного результата. Для этого подставим эти значения в исходную систему:

Вычисляя, получаем верные равенства.
4. Запишем приближенный ответ с точностью до сотых: ![]() ,
, ![]() ,
, ![]()
Задания 11-20. Даны векторы
![]() в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы ![]() образуют базис и найти координаты вектора
образуют базис и найти координаты вектора ![]() в этом базисе. Систему линейных уравнений решить по формулам Крамера.
в этом базисе. Систему линейных уравнений решить по формулам Крамера.
![]()
Решение
Решение. Для того, чтобы векторы ![]() образовывали базис, необходимо показать, что векторы некомпланарны, т. е. их смешанное произведение
образовывали базис, необходимо показать, что векторы некомпланарны, т. е. их смешанное произведение ![]() отлично от нуля.
отлично от нуля.
Вычислим смешанное произведение ![]() с помощью определителя третьего порядка:
с помощью определителя третьего порядка:
![]() =
= 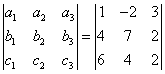 = -80.
= -80.
Поскольку ![]() = -80
= -80![]() 0, то векторы
0, то векторы ![]() образуют базис в пространстве R3.
образуют базис в пространстве R3.
Следовательно, любой вектор ![]() этого пространства единственным образом можно представить в виде
этого пространства единственным образом можно представить в виде ![]() =
=![]() , где
, где ![]() - координаты вектора
- координаты вектора ![]() в базисе
в базисе ![]() .
.
От векторного равенства перейдем к равенствам над соответствующими компонентами:
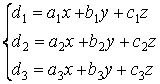 или
или 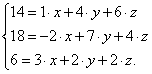
Получили систему трех линейных уравнений с тремя неизвестными ![]() координаты вектора
координаты вектора ![]() в новом базисе.
в новом базисе.
Решаем полученную систему методом Крамера, в соответствии с которым:
1) система трех линейных уравнений с тремя неизвестными имеет единственное решение, если ![]() - определитель третьего порядка, составленный из коэффициентов системы, не равен 0.
- определитель третьего порядка, составленный из коэффициентов системы, не равен 0.
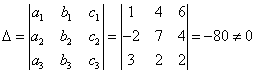
2) неизвестные ![]() находим по формулам Крамера
находим по формулам Крамера![]() ,
,
Где ![]() - определители третьего порядка, составленные из определителя системы
- определители третьего порядка, составленные из определителя системы ![]() заменой коэффициентов, стоящих в системе перед
заменой коэффициентов, стоящих в системе перед ![]() , свободными членами соответственно:
, свободными членами соответственно:
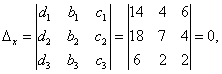
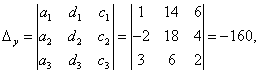
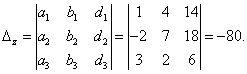
Тогда по формулам Крамера:![]()
Проверка 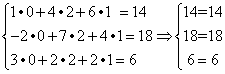
Получили тождества. Следовательно, система решена верно.
Ответ: 1) векторы ![]() образуют базис, 2) вектор
образуют базис, 2) вектор ![]() в базисе
в базисе ![]() имеет следующее разложение:
имеет следующее разложение: ![]() =
=![]() .
.
Задания 21-30. Даны координаты вершин пирамиды ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Найти: 1) площадь грани
. Найти: 1) площадь грани ![]() ;
;
2) объем пирамиды; 3) уравнения прямой ![]() ; 4) уравнение плоскости
; 4) уравнение плоскости ![]() ; 5) уравнения высоты
; 5) уравнения высоты ![]() , опущенной из вершины
, опущенной из вершины ![]() на грань
на грань ![]() ; 6) длину высоты
; 6) длину высоты ![]() ; 7) координаты точки пересечения высоты
; 7) координаты точки пересечения высоты ![]() с плоскостью
с плоскостью ![]() .
.
![]() (3;-1;2),
(3;-1;2), ![]() (-1;0;1),
(-1;0;1), ![]() (1;7;3),
(1;7;3), ![]() (8;5;8).
(8;5;8).
Решение
Координаты векторов
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
Здесь X, Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
A1A2(-4;1;-1)
A1A3(-2;8;1)
A1A4(5;6;6)
1) Для нахождения площади грани ![]() воспользуемся геометрическим смыслом модуля векторного произведения
воспользуемся геометрическим смыслом модуля векторного произведения ![]() , равного площади параллелограмма, построенного на векторах
, равного площади параллелограмма, построенного на векторах ![]()
![]() И
И ![]() как на сторонах.
как на сторонах.
Найдем векторное произведение
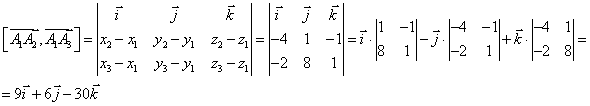 Тогда искомая площадь грани
Тогда искомая площадь грани ![]() равна:
равна:
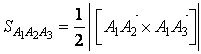 =
=![]() (ед2).
(ед2).
2) Объем пирамиды
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
Находим Определитель матрицы
∆ = (-4) • (8 • 6-6 • 1)-(-2) • (1 • 6-6 • (-1))+5 • (1 • 1-8 • (-1)) = -99
3) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
Уравнение прямой A1A2
4) Уравнение плоскости
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
Уравнение плоскости A1A2A3
(x-3)(1 • 1-8 • (-1)) - (y+1)((-4) • 1-(-2) • (-1)) + (z-2)((-4) • 8-(-2) • 1) = 9x + 6y - 30z-39 = 0
3x + 2y - 10z-13 = 0
5) Уравнение высоты пирамиды через вершину A4
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
![]()
6) Длина высоты пирамиды, проведенной из вершины A4
Расстояние d от точки M1(x1;y1;z1) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины:
![]()
7. Координаты точки пересечения высоты ![]() с плоскостью
с плоскостью ![]() .
.
Координаты точки пересечения высоты ![]() с плоскостью
с плоскостью ![]() получаются как результат решения системы, составленной из уравнения грани
получаются как результат решения системы, составленной из уравнения грани ![]() и уравнений высоты
и уравнений высоты ![]() .
.
Запишем уравнения высоты ![]() в параметрической форме:
в параметрической форме:
![]() , где t – параметр,
, где t – параметр,
Тогда 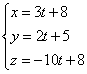 . Решая систему
. Решая систему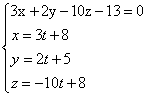 ,
,
Найдем значение параметра t. Подставляя выражения ![]() в первое уравнение, получим
в первое уравнение, получим
![]()
![]()
![]() .
.
Искомые координаты точки пересечения:
![]() ;
; ![]() ;
; ![]()
Задание 32. Найти проекцию точки ![]() на прямую, проходящую через точку
на прямую, проходящую через точку ![]() под углом 300 к оси Ох. Сделать чертеж.
под углом 300 к оси Ох. Сделать чертеж.
Решение
Сделаем чертёж
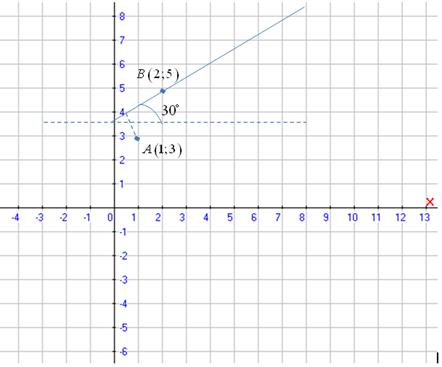
Сначала напишем уравнение прямой, проходящей через точки ![]() под углом 300 к оси Ох . Используем формулу y-y1=k(x-x1). Здесь x1=2, y1=5,
под углом 300 к оси Ох . Используем формулу y-y1=k(x-x1). Здесь x1=2, y1=5, ![]() .
.
Тогда ![]()
Теперь выпишем уравнение прямой, проходящей через точку ![]() перпендикулярно первой прямой
перпендикулярно первой прямой
![]() или
или ![]() .
.
Осталось найти точку пересечения первой и второй прямой. Эта точка и будет проекцией. Для этого надо решить систему уравнений
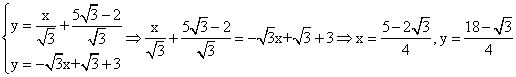
Отсюда ![]() .
.
Ответ: ![]() - проекция точки А.
- проекция точки А.
Задания 41-50. Вычислить пределы функций.
1. 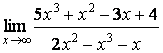
2. 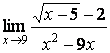
3. 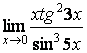
4. 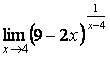
5. 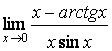
Решение
1. 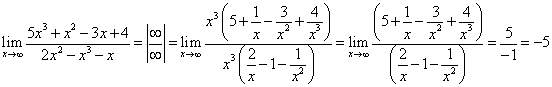
2. 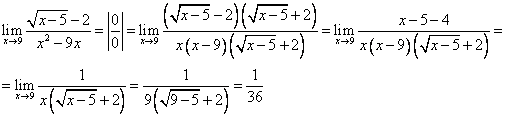
3. 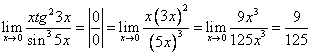
Использовали, ![]() при
при ![]()
4. 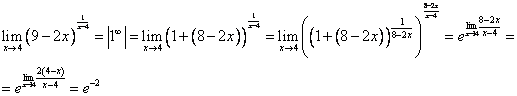
5. 
Задания 51-60. Найти производные ![]() следующих функций.
следующих функций.
1.  ;
;
2. 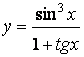
3.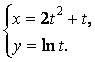
Решение
1. 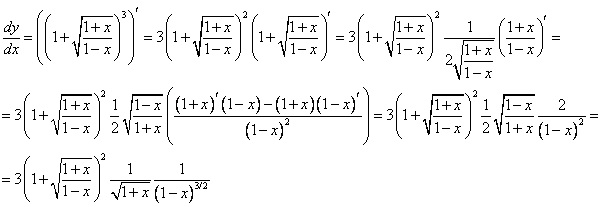 ;
;
2. 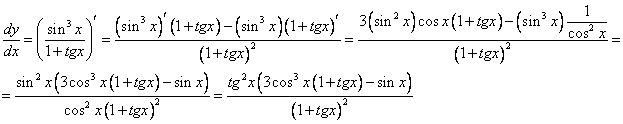 3.
3.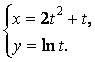
По формуле 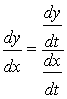 ,
, ![]() ,
, ![]() . Тогда
. Тогда 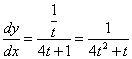
| < Предыдущая | Следующая > |
|---|