22. Предельные теоремы теории вероятностей

Делятся на две группы: Закон Больших Чисел (ЗБЧ) и Центральная Предельная Теорема (ЦПТ).

Закон Больших Чисел устанавливает связь между абстрактными моделями теории вероятностей и основными ее понятиями и средними значениями, полученными при статистической обработке выборки ограниченного объема из генеральной совокупности. P, F(x), M(x), D(x).

ЗБЧ доказывает, что средние выборочные значения при n®¥ стремятся к соответствующим значениям генеральной совокупности: hn(A)®P, Xср®M(X), sср2®D(X), F*(X)®F(X).

Лемма Маркова. Если Y – СВ, принимающая не отрицательные значения, то для любого положительного e:

P(Y³e)£M(x)/e, P(Y<e)³1-M(x)/e.

Доказательство. Рассмотрим Y и : Ye£Y, M(Ye)£M(Y)

M(Ye)=0×P(Y<e)+e×P(Y³e)=e×P(Y³e)

M(Y)³M(Ye)=e×P(Y³e).

Лемма позволяет сделать оценку вероятности наступления события по математическому ожиданию этой СВ.

Неравенство Чебышева. Для любой СВ с ограниченными первыми двумя моментами (есть МО и D) и для любого e>0:

Доказательство. По лемме Маркова: рассмотрим не отрицательную СВ Y

Y=(X-m)2 M(Y)=M(X-m)2=D(x)

P(|X-m|³e)=P((X-m)2³e2)=P(Y³e2)£M(Y)/e2=D(x)/e2.

Требуется только знание дисперсии СВ при любом законе распределения.

ЗБЧ в форме Чебышева. X1, X2, …, Xn – последовательность независимых СВ. Для любого e>0 и n®¥:

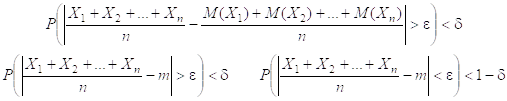
ЗБЧ в форме Бернулли. m – число успехов в серии из n последовательных испытаний Бернулли. P – вероятность успеха в каждом отдельном испытании. e>0:

ЗБЧ носит чисто качественный характер. В тех же условиях неравенство Чебышева позволяет получить количественную характеристику оценки вероятности.

Пример. Для определения вероятности события проведено 40000 опытов. События наблюдалось в m=16042 случаях. За вероятность события принимается относительная частота наступления события: m/n»0,4. Применяя неравенство Чебышева, оценить, с какой вероятностью можно гарантировать, что число 0,4, принятое за вероятность, отличается от истинной вероятности не больше, чем на 0,05.

Неизвестные p и q находим из системы уравнений:

=>

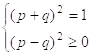< Предыдущая		Следующая >