21. Другие числовые характеристики СВ

Моменты распределения делятся на начальные моменты, центральные и смешанные.

1. Начальные моменты qго порядка (q=1,2,…): M(X1)=МО

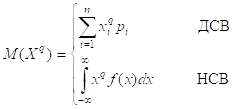
2. Центральные моменты qго порядка: M((X-m)2)=D

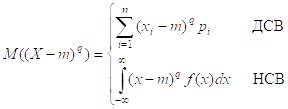
M(x-m)q=M(x)q-Cq1mM(x)q-1+ Cq2mM(x)q-2+…+(-1)qmq

M(x-m)3= M(x)3-3mM(x)2+2m3

M(x-m)2= M(x)2-m2=D(x)

Центральные моменты 3го и 4го порядков используются для получения коэффициентов асимметрии и эксцесса (As, Ex), характеризующих особенности конкретного распределения.

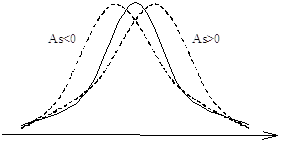
Для нормального закона распределения As=0.

Если As>0, то распределение имеет Правостороннюю скошенность. При As<0 – Левосторонняя скошенность.

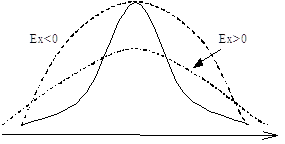
Эксцесс характеризует остро - или плосковершинность исследуемого распределения по сравнению с нормальным распределением.

НСВ:

1. Нормальное распределение: Ex=As=0

2. Равномерное распределение: As=0, Ex=-1,2

3. Экспоненциальное распределение: As=2, Ex=9.

Биноминальное:

3. Смешанные моменты:

Начальный смешанный момент порядка (k+s) системы 2х СВ (X+Y):

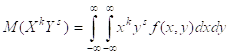
Центральный моменты порядка (k+s):

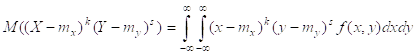
Центральный смешанный момент второго порядка:

Kxy=M((X-mx)(Y-my)) – корреляционный момент

– коэффициент корреляции

Мода ДСВ – значение СВ, имеющее максимальную вероятность.

Мода НСВ – значение СВ, соответствующее максимуму функции плотности вероятности f(x).

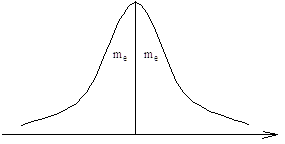Обозначение моды: m0, M0(x), mod(x).

Медиана СВ Х (me, Me(x), med(x)) – значение СВ, для которого выполняется равенство:

P(X<me)=P(X>me)

F(me)=0,5.

Медиана – это площадь, получаемая делением фигуры пополам.

В симметричном распределении m=m0=me. В несимметричном они не равны.

Так как мода и медиана зависят от структуры распределения, их называют Структурными средними.

Медиана – это значение признака, который делит ранжированный ряд значений СВ на две равных по объему группы. В свою очередь, внутри каждой группы могут быть найдены те значения признака, которые делят группы на 4 равные части – Квартиль.

Ранжированный ряд значений СВ может быть поделен на 10 равных частей – децилей, на 100 – центилей.

Такие величины, делящие ранжированный ряд значений СВ на несколько равных частей, называются Квантилями.

Под p% квантилями понимаются такие значения признака в ранжированном ряду, которые не больше p% наблюдений.

< Предыдущая		Следующая >