Ряды с неотрицательными членами.

Теорема 2.1. Пусть все члены ряда неотрицательны: , . Для того, чтобы ряд сходился, необходимо, чтобы последовательность его частичных сумм была ограничена сверху и достаточно, чтобы была ограничена сверху хотя бы одна подпоследовательность последовательности его частичных сумм.

Пример 2.1. Доказать, что если ряд , где , , сходится, то ряд также сходится.

Решение. Пусть - последовательность частичных сумм первого ряда, а - второго ряда. Согласно теореме 2.1 (необходимость) из сходимости первого ряда следует, что последовательность ограничена сверху. Тогда ограничена сверху и последовательность : . Отсюда в силу условия следует, что

для всех . Поэтому ограничена сверху последовательность . Применив теорему 2.1 (достаточность), мы видим, что сходится ряд .

Пример 2.2. Доказать, что ряд расходится.

Решение. Данный ряд состоит из положительных членов: , . В силу очевидного неравенства.

, ,

Последовательность частичных сумм ряда не ограничена сверху. Согласно теореме 2.1 это и означает расходимость данного ряда.

Пример 2.3. Если и , , то ряд сходится или расходится одновременно с рядом .

Решение. Пусть и - частичные суммы данных рядов. Поскольку , , то

,

,

,

.

Сложив эти неравенства почленно, получим

, т. е.

. (2.1)

Если ряд сходится, то по теореме 2.1 последовательность ограничена сверху. В силу неравенства (2.1) ограничена сверху подпоследовательность последовательности частичных сумм ряда . Согласно теореме 2.1 этот ряд сходится.

С другой стороны, справедливы неравенства

,

,

,

Сложив эти неравенства почленно, получим , Т. е.

(2.2)

Если ряд расходится, то (теорема 2.1) последовательность его частичных сумм не ограничена сверху. В силу неравенства (2.2) тогда не ограничена сверху и подпоследовательность . Отсюда следует расходимость ряда .

Пример 2.4. Исследовать на сходимость ряд .

Решение. Если , то , . Поэтому не выполняется необходимое условие (1.5) сходимости ряда. Следовательно, при данный ряд расходится. Пусть . Тогда и , . Согласно примеру 2.1 исследуемый ряд сходится или расходится одновременно с рядом , т. е. с рядом

, (2.3)

Где . Если , то и, как установлено в примере 1.5, ряд (2.3) сходится.

Если , то и ряд (2.3) расходится.

Итак, ряд сходится при и расходится при .

Ряд называется гармоническим. Поскольку для него , то этот ряд расходится.

Мажорантный признак сравнения. Пусть существует номер такой, что для всех справедливы неравенства . Тогда 1) из сходимости ряда следует сходимость ряда ; 2) из расходимости ряда следует расходимость ряда .

Пример 2.5. Исследовать на сходимость ряд .

Решение. Поскольку для любого натурального числа справедливы неравенства , а ряд сходится (см. пример 1.5), то на основании мажорантного признака сравнения данный ряд сходится.

Пример 2.6. Исследовать на сходимость ряд .

Решение. Заметим, что при справедливо неравенство . Поэтому , . Так как гармонический ряд расходится (см. пример 2.4), то в силу теоремы 1.1 ряд также расходится. Значит, согласно мажорантному признаку расходится и исследуемый ряд.

Пример 2.7. Исследовать на сходимость ряд .

Решение. Имеем: , . Значит, при . Ряд с общим членом сходится, как это было установлено в примере 2.4. Поэтому сходится и данный ряд.

Пример 2.8. Доказать, что сходится ряд .

Решение. Сначала докажем, что при справедливо неравенство

. (2.4)

Для этого рассмотрим функцию , . Ее производная . Легко видеть, что при , при . Значит, - наибольшее значение функции . Поэтому при , и неравенство (2.4) доказано. Их этого неравенства следует, что . Поэтому , . Снова использовав (2.4), получаем

.

Значит, , . Таким образом, , . Ряд , как уже отмечалось, сходится. Следовательно, данный ряд сходится.

При исследовании рядов, общий член которых содержит логарифмическую функцию, бывает полезным

Утверждение 2.1. Пусть , . Тогда существует такое натуральное число , что при

. (2.5)

Для доказательства этого утверждения, покажем, что

. (2.6)

Если , то равенство (2.6) верно, поскольку , , а , т. к. . Пусть . Рассмотрим предел . Сделав в нем замену , получим . Положим . Применим правило Лопиталя раз:

,

Т. к. . Итак, равенство (2.6) доказано. Согласно определению предела числовой последовательности, для найдется такой номер , что при справедливо неравенство , т. е. . Утверждение доказано.

Пример 2.9. Доказать, что ряд расходится.

Решение. Применяя неравенство (2.5), взяв в нем вместо , , , мы видим, что при . Значит, при

, т. е. , .

Поскольку ряд расходится, то расходится и исследуемый ряд.

Пример 2.10. Исследовать на сходимость ряд , .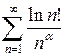

Решение. При справедливо неравенство . Поэтому и, следовательно,

, .

При , и ряд расходится (см. пример 2.4). Тогда расходится ряд (теорема 1.1). Из неравенства , Согласно мажорантному признаку сравнения получаем, что при данный ряд расходится.

Пусть . Тогда найдется число такое, что . Применив неравенство (2.5) для этого и , получим: при . Тогда , и ряд сходится (пример 2.4). Из неравенств согласно мажорантному признаку сравнения следует, что при данный ряд сходится.

Пример 2.11. Исследовать на сходимость ряд , где - число цифр числа .

Решение. Сначала получим формулу для . Поскольку - число цифр числа , то , откуда логарифмируя, получаем: . Значит, , т. е. . Очевидно, что . Итак, получена оценка: , из которой следует, что

. (2.7)

Рассуждая как при решении примера 2.10, легко установить, что сходится ряд . Как уже упоминалось, сходится ряд . Согласно теореме 1.1 сходится ряд . Наконец, из неравенства (2.7) следует сходимость ряда .

Упражнения.

Используя мажорантный признак сравнения, исследовать на сходимость ряды 2.1-2.6:

2.1. . Ответ: сходится.

2.2 . Ответ: расходится.

2.3. . Ответ: сходится.

2.4. . Ответ: сходится.

2.5. . Ответ: расходится.

2.6. . Ответ: сходится.

2.7. Пусть ряд , где , , сходится. Доказать, что сходится ряд . Указание: применить неравенство .

Признак сравнения в предельной форме. Пусть даны ряды и , где , , , и , . Тогда 1) если и сходится ряд , то сходится ряд ; 2) если и расходится ряд , то расходится . Таким образом, при оба ряда одновременно сходятся или расходятся.

Следствие 1. Пусть , , , и при , т. е. . Тогда ряды и сходятся или расходятся одновременно.

Следствие 2. Пусть , и существуют числа и такие, что при . Тогда ряд сходится, если и расходится, если .

Пример 2.12. Исследовать на сходимость ряд .

Решение. Пусть , , . При решении примера 1.10 было установлено, что . Поэтому . Поскольку ряд расходится. То согласно признаку сравнения в предельной форме данный ряд расходится.

Пример 2.13. Исследовать на сходимость ряд .

Решение. Пусть , . Известно, что при . Кроме того, (см. утверждение 1.1). Поэтому при и, следовательно, при , где , . Ряд сходится (см. пример 1.5). В силу следствия 1 данный ряд сходится.

Пример 2.14. Исследовать на сходимость ряд , где , .

Решение, Имеем:

, . (2.8)

Поступая также, как при решении примера 1.10, получим:

И, аналогично, . Поэтому (см. (2.8)) при . Ряд сходится при (см. пример 2.4). Согласно следствию 2 данный ряд сходится при .

При исследовании рядов, члены которых содержат факториалы, иногда бывает полезной формула Стирлинга:

при .

Пример 2.15. Исследовать на сходимость ряд .

Решение. Применив формулу Стирлинга: при . Ряд сходится при (см. пример 2.4). В силу следствия 2 исследуемый ряд сходится при .

Упражнения.

Используя признак сравнения в предельной форме, исследовать на сходимость ряды:

2.8. . Ответ: сходится.

2.9. . Ответ: сходится.

2.10. . Ответ: сходится.

2.11. . Ответ: сходится, если и расходится, если .

2.12. . Ответ: сходится, если и расходится, если .

2.13. . Ответ: сходится, если и расходится, если .

Признак Даламбера. Ряд , 1) сходится, если существуют такие и , что для всех , в частности, если ; 2) расходится, если для всех , в частности, если .

Если , то ряд может как сходится, так и расходится.

Следствие. Пусть , и существует . Тогда при ряд сходится, а при - расходится. При ряд может как сходится, так и расходится.

Пример 2.16. Исследовать на сходимость ряд .

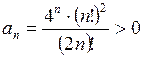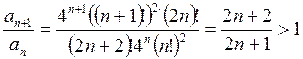Решение. Имеем: , . Поскольку для всех , то согласно признаку Даламбера ряд расходится.

Пример 2.17. Исследовать на сходимость ряд .

Решение. Имеем: , , . Значит, , и в силу следствия признака Даламбера ряд расходится.

Пример 2.18. Исследовать на сходимость ряд .

Решение. Имеем: , , и поэтому ряд сходится.

Пример 2.19. Исследовать на сходимость ряд .

Решение. Имеем: 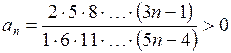, , . Значит, . Поскольку , то ряд сходится.

Пример 2.20. Исследовать на сходимость ряд .

Решение. Имеем , , 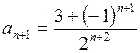. Пусть . Все члены последовательности содержатся в последовательностях и . Поэтому , . Значит, , и признак Даламбера ответа не дает. Данный ряд можно исследовать с помощью приводимого ниже радикального признака Коши.

Упражнения.

Используя признак Даламбера, исследовать на сходимость ряды:

2.14. . Ответ: расходится.

2.15. . Ответ: сходится.

2.16. . Ответ: сходится.

2.17. . Ответ: сходится.

2.18. . Ответ: сходится.

2.19. . Ответ: расходится.

2.20. . Ответ: сходится.

Радикальный признак Коши. Ряд , , 1) сходится, если существуют такие и , что для всех , в частности, если ; 2) расходится, если для всех , в частности, если .

Если , то ряд может как сходится, так и расходится.

Следствие. Пусть , , и существует . Тогда при ряд сходится, а при - расходится. При ряд может как сходится, так и расходится.

Пример 2.21. Исследовать на сходимость ряд .

Решение. Общий член данного ряда можно записать в виде

.

Ясно, что

.

Значит, для всех , где . Согласно радикальному признаку Коши ряд сходится.

Пример 2.22. Исследовать на сходимость ряд .

Решение. Имеем: , ,

.

Значит, , и согласно следствию радикального признака Коши ряд сходится.

Пример 2.23. Исследовать на сходимость ряд .

Решение. Пусть . Имеем: , т. к. и, аналогично, . Поскольку , то . Значит, ряд сходится.

Упражнения.

Используя радикальный признак Коши, исследовать на сходимость ряды:

2.21. . Ответ: сходится.

2.22. . Ответ: сходится.

2.23. . Ответ: сходится.

2.24. . Ответ: сходится.

2.25. . Ответ: сходится.

2.26. . Ответ: расходится.

2.27. 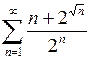. Ответ: сходится.

Интегральный признак Коши. Если функция неотрицательна и убывает на промежутке , где , то ряд

И несобственный интеграл

Сходятся или расходятся одновременно.

Пример 2.24. Исследовать на сходимость ряд .

Решение. Рассмотрим функцию при . Ясно, что и при , т. е. убывает на промежутке . Исследуем на сходимость несобственный интеграл:

.

Значит, несобственный интеграл сходится и согласно интегральному признаку Коши сходится и данный ряд.

Пример 2.25. Исследовать на сходимость ряд , .

Решение. Пусть , . При справедливо неравенство и, следовательно, . Пусть - наибольшие из чисел: 2 и . Поскольку функция положительна и убывает на промежутке , то для исследования ряда на сходимость можно применить интегральный признак Коши. При . Если , то и . Если , то и . При и . Значит, несобственный интеграл сходится при и расходится при .

Пример 2.26. Исследовать на сходимость ряд .

Решение. Поскольку при , то и, стало быть, . Ряд расходится (см. пример 2.25). Согласно мажорантному признаку сравнения данный ряд расходится.

Пример 2.27. Исследовать на сходимость ряд , .

Решение. Если , то . Поэтому не выполнено условие (1.5) и ряд расходится.

Пусть . Рассмотрим функцию на промежутке . Имеем: при . Функция положительна и убывает на промежутке . Исследуем на сходимость несобственный интеграл . Для этого найдем интеграл . Пусть . Применим формулу интегрирования по частям , положив , . Тогда , и . Поэтому

.

Если , то и согласно (2.6) предел существует и конечен. При этот предел бесконечен. При имеем:

.

Итак, несобственный интеграл и, следовательно, данный ряд сходятся при и расходятся при .

Пример 2.28. Исследовать на сходимость ряд .

Решение. Пусть . Если , то, очевидно, и ряд расходится. Пусть . Тогда согласно (2.6) . Поэтому можно применить эквивалентность при , взяв . Имеем: при . Значит, . Использовав следствие 1 признака сравнения в предельной форме и пример 2.27, получаем, что данный ряд сходится при .

Пример 2.29. Пусть , , и . Доказать, что ряд сходится.

Решение. Выберем число так, что . Из определения верхнего предела следует, что найдется такое натуральное число , что при . Значит, . Поскольку , то получаем: . Поскольку , то . Но тогда, как установлено в примере 2.25, сходится ряд . Поэтому в силу мажорантного признака сравнения сходится ряд .

Упражнения.

Используя интегральный признак Коши, исследовать на сходимость ряды:

2.28. . Ответ: расходится.

2.29. . Ответ: расходится.

2.30. . Ответ: сходится.

2.31. 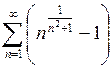. Ответ: сходится.

2.32. . Ответ: ряд сходится при любом , если , и при , если ; ряд расходится при любом , если , и при , если .

< Предыдущая		Следующая >