13.03. Задачи и размышления
Рассмотрим некоторые проблемы математического моделирования полета искусственных спутников. Найдем зависимость скорости искусственного спутника от высоты его полета над поверхностью Луны. Применим в дальнейшем эту модель для расчета скорости движения Луны вокруг Земли.
Выдвинем следующие гипотезы:
1. Спутник движется вокруг Луны по окружности (эта гипотеза может быть далека от истины в случае экcцентрической орбиты).
2. Сила притяжения спутника Луной обратно пропорциональна квадрату расстояния от центра Луны (на чем основана эта гипотеза?).
3. Притяжением спутника Землей пренебрегаем (всегда ли оправдана эта гипотеза?).
Пусть спутник движется со скоростью V по окружности на высоте h над поверхностью Луны ( рис. 11.26).
|
Рис. 11.26. Взаимное расположение Луны |
Закон всемирного тяготения имеет вид:
![]() ,
,
Где МЛ – Масса Луны; m – масса спутника; G – гравитационная постоянная, равна ![]() Н×м2/кг2; R – радиус Луны, равен 1738 км. Используем второй закон Ньютона:
Н×м2/кг2; R – радиус Луны, равен 1738 км. Используем второй закон Ньютона:
![]()
Тогда
![]()
После преобразований получаем:
![]() .
.
1. Исходя из физической сути параметра h, найдите область его допустимых значений. Исследуйте зависимость ![]() . Если с высоты
. Если с высоты ![]() спутник опустить на более низкую высоту
спутник опустить на более низкую высоту ![]() , отличающуюся от
, отличающуюся от ![]() на 1%, то на сколько должна возрасти скорость V, чтобы "удержать" спутник на орбите? Проведите расчеты точно и приближенно с помощью дифференциала. При
на 1%, то на сколько должна возрасти скорость V, чтобы "удержать" спутник на орбите? Проведите расчеты точно и приближенно с помощью дифференциала. При ![]() Км оцените погрешность приближенных вычислений.
Км оцените погрешность приближенных вычислений.
Формула вычисления скорости V позволяет получить интересное следствие. С ее помощью можно найти первую космическую скорость для Луны – такую скорость, которую нужно сообщить спутнику у поверхности для того, чтобы он двигался по окружности, не падая на Луну. Такой результат может быть получен при ![]() :
:
V=1,7 Км/c.
Для сравнения отметим, что для Земли первая космическая скорость – 7,9 км/c.
Рассмотренная математическая модель весьма универсальна. Вместо Луны могут рассматриваться какие угодно космические тела, а спутники могут быть естественные и искусственные. Так, при движении спутника по круговой орбите вокруг Земли его скорость
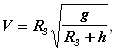
Где ![]() Км/c2 – Ускорение силы тяжести Земли;
Км/c2 – Ускорение силы тяжести Земли; ![]() – радиус Земли;
– радиус Земли; ![]() Км.
Км.
Интересно, что исследуемая скорость V вовсе не зависит от массы спутника. Если теперь рассматриваемую модель применить для вычисления скорости движения Луны вокруг Земли, то получим, что
V=1 км/c.
По этой же модели легко вычислить скорость движения Земли вокруг Солнца. Она равна 30 км/с.
2. Человек, находящийся в кабине искусственного спутника Земли, пребывает в состоянии невесомости. На каких высотах следовало бы лететь самолету, чтобы при "дозвуковых" скоростях добиться искусственной невесомости? Что эффективнее с точки зрения технических возможностей: увеличивать скорость самолета или его высоту для достижения искусственной невесомости?
3. Ученые подсчитали, что угловая скорость вращения Земли вокруг своей оси равна 0,00007 1/c. Какой должна быть орбита искусственного спутника Земли, чтобы он казался неподвижным для наблюдателя с Земли ("зависал" в небе)?
4. Один из возможных проектов космического телевидения предполагает использование трех неподвижных относительно Земли искусственных спутников, образующих равносторонний треугольник (рис.11.27). Работая как ретрансляционные станции, они посылают волны, которые, распространяясь прямолинейно, достигнут любой точки земной поверхности.
|
Рис. 11.27. Возможная схема международного |
Не "заслонит" ли Земля на высоте "зависания" источник происхождения волн? Может ли при этом возникнуть необходимость в другой схеме расположения спутников? Можно ли использовать Луну для подобного технического проекта космического телевидения, учитывая, что она "достаточно высока" и всегда повернута одной стороной к Земле?
5. Напряженность поля тяготения ![]() на высоте h от поверхности Земли определяется по формуле:
на высоте h от поверхности Земли определяется по формуле:
![]()
Где ![]() - напряженность на поверхности Земли, а R - радиус Земли. При h<<R пользуются упрощенной формулой:
- напряженность на поверхности Земли, а R - радиус Земли. При h<<R пользуются упрощенной формулой:
![]()
Как получена эта формула? Целесообразно ли пренебречь вторым слагаемым в скобках для еще большего упрощения формулы? Не произойдет ли при этом значительной утраты ее физического содержания?
6. Среднее расстояние от Земли до Луны –![]() Км. На каком расстоянии от центра Земли силы притяжения между Землей и Луной будут равны по модулю между собой, если масса Земли равна
Км. На каком расстоянии от центра Земли силы притяжения между Землей и Луной будут равны по модулю между собой, если масса Земли равна ![]() Кг, Луны –
Кг, Луны – ![]() Кг? Сколько решений имеет задача? Абсолютная погрешность, с которой найдена масса Луны, составляет
Кг? Сколько решений имеет задача? Абсолютная погрешность, с которой найдена масса Луны, составляет ![]() Кг, то есть истинная масса Луны располагается в промежутке:
Кг, то есть истинная масса Луны располагается в промежутке:
![]() Кг
Кг ![]()
![]()
![]() Кг.
Кг.
Оцените с помощью дифференциала возникающую при этом погрешность в определении искомого расстояния.
|
Рис. 11.28. Положение |
7. Шар массой m и радиусом r подвешен на нити длиной l к вертикальной стене (рис.11.28).
Сила натяжения нити по модулю равна
![]()
А модуль силы реакции нити равен
![]()
Какие физические гипотезы приняты при выводе этих формул? Какие возможны математические упрощения данных формул, если точность результатов, необходимая на практике, составляет a%? Исследуйте зависимости:

Для отыскания наибольшего и наименьшего значений функции могут быть применены весьма неожиданные подходы. Вот один из них.
Известно, что скалярное произведение векторов ![]() и
и ![]() определяется по формуле:
определяется по формуле:
![]()
Где J – угол между векторами.
Так как
-1 £ cosj £ 1,
То справедливо двойное неравенство
![]()
Знак равенства достигается, когда векторы коллинеарны, причем
![]()
Если векторы при этом одинаково ориентированы, и
![]()
Если они направлены в противоположные стороны.
В координатной форме мы получим следующее двойное неравенство:
![]()
Известно также, что коллинеарные векторы связаны соотношением
![]()
Или в координатной форме
![]()
Воспользуемся этими фактами для нахождения наибольшего значения функции
![]()
![]()
Очевидно, эта функция определена и непрерывна на отрезке [-8;5], следовательно, она достигает на нем своего наибольшего и наименьшего значений. Введем в рассмотрение векторы
![]()
![]()
Тогда
![]()
![]()
![]()
Знак равенства достигается, когда векторы ![]() и
и ![]() коллинеарны и сонаправлены. Это возможно, когда
коллинеарны и сонаправлены. Это возможно, когда
![]()
5–x = x+8 ;
X = –1,5.
Итак, наибольшее значение ![]() .
.
Отметим, что нижняя оценка данной функции, получаемая таким способом, слишком груба :
![]()
В то время как очевидна более точная оценка:
![]()
Рассмотрим другой пример. Найдем наибольшее значение функции
![]()
Проводим рассуждения аналогично. Находим область допустимых значений:
![]()
Вводим в рассмотрение векторы (почему?):
![]() ,
, ![]()
Тогда
![]()
![]()
Значит,
![]()
Определим значение аргумента х, при котором достигается наибольшее значение функции из условия коллинеарности векторов:
![]()
Установим, лежит ли эта точка в области определения функции, проверив условие
![]()
Получим:
![]()
Что подтверждает ее принадлежность этой области определения.
Таким образом, наибольшее значение функции
![]()
Достигается при ![]()
8. Решение этих двух примеров основано на использовании некоторых общих закономерностей. Выявите эти закономерности и сформулируйте их в виде теоремы, позволяющей исследовать на наибольшее и наименьшее значения некоторый класс функций.
9. В DABC AB=c; BC=a; ÐBAC=a; ÐABC=b имеет место следующая формула:
![]()
Исследуйте функции ![]() ;
; ![]() и
и ![]() . Достигают ли они в своих областях определения наибольшего и наименьшего значений? Угол b измеряется в градусах с абсолютной погрешностью в 1°. Оцените с помощью дифференциала, какой будет погрешность вычисления угла a при фиксированном с и различных значениях a. Удастся ли повысить точность вычисления угла a, если измерять угол b с точностью до 0,01 рад?
. Достигают ли они в своих областях определения наибольшего и наименьшего значений? Угол b измеряется в градусах с абсолютной погрешностью в 1°. Оцените с помощью дифференциала, какой будет погрешность вычисления угла a при фиксированном с и различных значениях a. Удастся ли повысить точность вычисления угла a, если измерять угол b с точностью до 0,01 рад?
10. Две функции имеют одинаковое приращение при одинаковом приращении аргумента. Равны ли они тождественно?
11. Привести пример физического процесса, для которого целесообразно применить теорему Лагранжа с целью изучения этого процесса.
12. Космонавт видит Землю под углом a, с высоты h. Какой будет площадь поверхности Земли S, которую он наблюдает? Как изменится эта площадь при уменьшении высоты на величину 1 км? (Вычислить точно и оценить с помощью дифференциала.) Как зависит уменьшение этой площади от высоты полета h? Какие упрощающие гипотезы можно сделать при решении задачи, если h – высота многоэтажного дома? Исследуйте зависимость максимальной видимой площади поверхности Земли:
– от высоты;
– от угла зрения, под которым она видна.
13. Приведите примеры физических процессов, которые обладают свойством асимптотичности.
|
Рис. 11.29. Зависимость напряжения пробоя между |
14. Зависимость напряжения пробоя между плоскими электродами от величины pd (p – давление газа, d - расстояние между электродами), представлена на рис.11.29.
Представьте это семейство кривых в виде одного аналитического выражения, зависящего от одного или двух параметров.
15. Напряженность магнитного поля Земли на больших высотах изображена графически на рис.11.30.
Попробуйте задать эту функцию приближенно одним аналитическим выражением так, чтобы график приближенного задания удовлетворял условиям:
A) располагался как можно ближе к данной кривой, оставаясь выше ее, и касался кривой разве что в точках экстремума;
Б) график приближенно заданной функции совпадал с данной кривой в точках экстремума, а при расстоянии от центра Земли 12800 км (удвоенный радиус Земли) скорости изменения напряженности по графику и по приближенной формуле совпадали.
|
Рис. 11.30. Напряженность магнитного поля Земли |
16. Около равнобедренного треугольника описана окружность радиуса R И в него вписана окружность радиуса r. Угол при его основании равен a. Исследуйте зависимости ![]() . Найдите наименьшее и наибольшее значения площади этого треугольника при изменении r.
. Найдите наименьшее и наибольшее значения площади этого треугольника при изменении r.
17. Изготовление цилиндрических деталей на трехвалковом стане схематично изображено на рис.11.31.
Прямоугольная заготовка проходит между тремя валками, из которых два нижних неподвижны, а верхний может опускаться и подниматься. На какое расстояние следует опустить верхний валик, чтобы получить цилиндр нужного диаметра? Исследуйте зависимость этого расстояния:
А) от расстояния между нижними валками;
Б) от радиуса валков;
В) от радиуса изготовляемой цилиндрической детали.
Какая погрешность возможна в вертикальном перемещении валка, если допустимая погрешность радиуса изготовляемого цилиндра не превосходит 1%?
|
Рис. 11.31. Схема изготовления цилиндрической |
|
|
18. При измерении диаметра очень больших деталей иногда поступают так: замеряют размеры a и b (рис.11.32), далее находят диаметр d, Пользуясь геометрическими соображениями. При одинаковой абсолютной погрешности измерения величины a и b оценить, какой из этих параметров в большей степени влияет на абсолютную погрешность при вычислении диаметра.
19. Груз массы m подвешен на нити длиной l. Его отклоняют в горизонтальное положение, сохраняя натяжение нити, и отпускают. Каким будет максимальное натяжение при движении груза? Когда проекция скорости на вертикальное направление наибольшая? Какие физические гипотезы можно принять при создании математической модели? Насколько они упростят или же усложнят решение задачи?
20. Биссектриса прямоугольного треугольника делит катет на отрезки a и b (a>b). Достигает ли ее длина своего наибольшего и наименьшего значений при всех возможных изменениях a? Изобразите семейство этих треугольников. Как удобнее такие треугольники построить? Каким будет приращение биссектрисы при изменении a от 1,16b до 1,1b? Оцените это приращение приближенно с помощью дифференциала и по теореме Лагранжа. Дайте геометрическую интерпретацию такому приближению.
21. Круг перемещается по прямой l. Сформулируйте физическую задачу, в которой можно было бы использовать математическое описание предыдущей.
22. В некотором государстве инфляция составляет a% в день. Один из банков этого государства принимает вклады до востребования под b% годовых. На какой срок следует разместить вклад, чтобы реальный доход по нему был наибольшим? Если инфляция сохранит свой темп, что произойдет с этим вкладом? Можно ли "преодолеть " инфляцию при достаточно высоком годовом банковском проценте? Какой срок хранения денег в банке следует считать:
- наиболее благоприятным для вкладчика;
- допустимым для данного банка?
23. Найти наибольшее и наименьшее значения функции
![]()
При ![]() .
.
Данная функция непрерывна на отрезке ![]() , поэтому достигает на нем своего наибольшего и наименьшего значений. Однако традиционная схема нахождения этих значений, возможно, осложнится уже при отыскании первой производной
, поэтому достигает на нем своего наибольшего и наименьшего значений. Однако традиционная схема нахождения этих значений, возможно, осложнится уже при отыскании первой производной![]() . Эта трудность преодолима, если перейти к параметрическому заданию данной функции.
. Эта трудность преодолима, если перейти к параметрическому заданию данной функции.
Пусть
![]() ,
,
Тогда
![]()
Поэтому
![]() .
.
![]() терпит разрыв при
терпит разрыв при ![]() . В этом случае
. В этом случае
![]() .
.
Находим
![]()
Это и будет, соответственно, наименьшим и наибольшим значениями функции.
24. Приведите примеры функции, при исследовании которых их параметризация упрощает преобразования.
Свойство монотонности функции может быть использовано весьма неожиданно.
Что больше:
![]() или
или ![]() ?
?
Ясно, что простым вычислительным экспериментом, даже с использованием ЭВМ, на этот вопрос ответить трудно. А между тем решение задачи можно провести в достаточно общем виде.
Рассмотрим функцию
![]()
Ее производная
![]()
Положительна при ![]() , равна нулю при
, равна нулю при ![]() и отрицательна при
и отрицательна при ![]() . Это значит, что функция
. Это значит, что функция ![]() возрастает на промежутке
возрастает на промежутке ![]() и убывает на промежутке
и убывает на промежутке ![]() . Поэтому для чисел X и Y, удовлетворяющих условию
. Поэтому для чисел X и Y, удовлетворяющих условию ![]() , имеем:
, имеем:
![]()
Или
![]()
Если же ![]() , то
, то
![]()
А значит
![]()
Возвращаясь к сравнению величин ![]() и
и ![]() , легко установить:
, легко установить:
![]() ,
,
Поэтому
![]()
![]()
Пользуясь рассмотренным методом, можно, например, доказать, что
![]()
Или
![]()
( G – ускорение свободного падения).
25. Какую сравнительную оценку можно сделать, применяя идею решения предыдущей задачи, для функции
![]() ?
?
Приведите свои примеры, в которых рассмотренный прием был бы целесообразен.
| < Предыдущая | Следующая > |
|---|
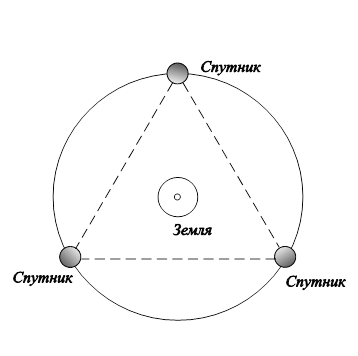
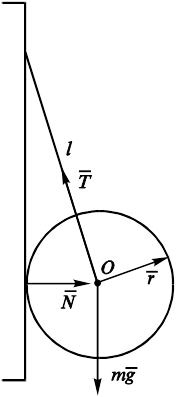
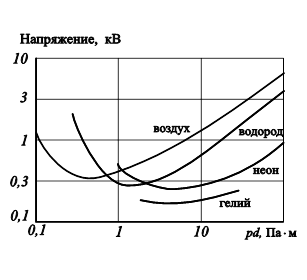
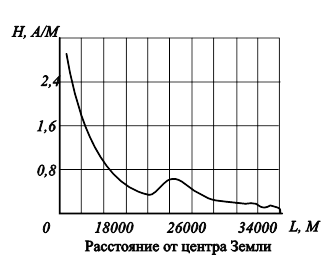
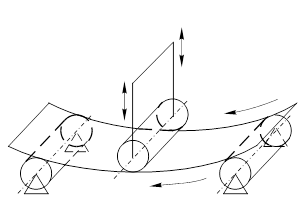
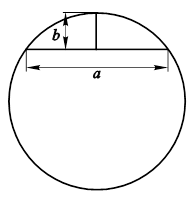 Рис. 11.32. Косвенные замеры для определения диаметра очень больших деталей.
Рис. 11.32. Косвенные замеры для определения диаметра очень больших деталей.