Вариант № 08
В задачах 1-9 найти общие решения уравнений и частные решения, если есть начальные условия.
1. ![]() . Уравнение является однородным. Сделаем замену
. Уравнение является однородным. Сделаем замену ![]() Тогда
Тогда ![]() . Получим уравнение
. Получим уравнение ![]() , или
, или ![]() . Запишем
. Запишем
Уравнение в дифференциалах: ![]() . Разделяем переменные:
. Разделяем переменные: ![]() . Интегрируем уравнение:
. Интегрируем уравнение: ![]() . Получим:
. Получим: ![]() . Потенцируем:
. Потенцируем: ![]() . Потенцируем ещё раз:
. Потенцируем ещё раз: ![]() . Вернёмся к переменной Y, делая обратную замену U=Y/X:
. Вернёмся к переменной Y, делая обратную замену U=Y/X: ![]() . Определим постоянную С из начальных условий:
. Определим постоянную С из начальных условий: ![]() , отсюда C=1. Подставляя это значение в общее решение, получим частное решение:
, отсюда C=1. Подставляя это значение в общее решение, получим частное решение: ![]() . Ответ:
. Ответ: ![]() (в неявном виде это выглядит так:
(в неявном виде это выглядит так: ![]() ).
).
2. ![]() . Уравнение является линейным. Решим его методом Бернулли. Будем искать решение в виде произведения Y=U∙V, где U и V неизвестные функции, определяемые в данном случае уравнениями
. Уравнение является линейным. Решим его методом Бернулли. Будем искать решение в виде произведения Y=U∙V, где U и V неизвестные функции, определяемые в данном случае уравнениями ![]() и
и ![]() или
или ![]() . Решим первое уравнение:
. Решим первое уравнение: ![]() или
или ![]() . Отсюда
. Отсюда ![]() (произвольная постоянная добавляется при решении второго уравнения). Потенцируя, находим:
(произвольная постоянная добавляется при решении второго уравнения). Потенцируя, находим: ![]() . Подставим найденную функцию U во второе уравнение и решим его:
. Подставим найденную функцию U во второе уравнение и решим его: ![]() или
или ![]() . Тогда
. Тогда
![]() . Таким образом, общее решение имеет вид:
. Таким образом, общее решение имеет вид: ![]() . Найдём C, исходя из начальных условий:
. Найдём C, исходя из начальных условий: ![]() . Тогда
. Тогда ![]() . Таким образом, частное решение есть
. Таким образом, частное решение есть ![]() . Ответ:
. Ответ: ![]() .
.
3. ![]() . Это уравнение Бернулли. Его можно решать непосредственно как линейное уравнение, применяя метод вариации произвольной постоянной. Решим однородное уравнение:
. Это уравнение Бернулли. Его можно решать непосредственно как линейное уравнение, применяя метод вариации произвольной постоянной. Решим однородное уравнение: ![]() или
или ![]() . Отсюда находим
. Отсюда находим ![]() . Будем предполагать, что решение исходного уравнения имеет
. Будем предполагать, что решение исходного уравнения имеет
такую же структуру, но C=C(X), т. е. ![]() , где C(X) – некоторая неизвестная функция. Определим эту функцию, подставляя данное (предполагаемое) решение в исходное уравнение. Найдём
, где C(X) – некоторая неизвестная функция. Определим эту функцию, подставляя данное (предполагаемое) решение в исходное уравнение. Найдём ![]() .
.
Тогда ![]() . Или
. Или ![]() . Разделяем переменные:
. Разделяем переменные: ![]() . Интегрируем уравнение:
. Интегрируем уравнение:![]() . Следовательно,
. Следовательно, ![]() . Общие решение уравнения
. Общие решение уравнения ![]() . Воспользуемся начальными условиями:
. Воспользуемся начальными условиями: ![]() , т. е. C1=2/3. Тогда частным решением будет
, т. е. C1=2/3. Тогда частным решением будет ![]() или
или ![]() . Ответ:
. Ответ: ![]() .
.
4. ![]() .
.
Найдём частные производные: ![]() ,
, ![]() . Следовательно, уравнение является уравнением в полных дифференциалах. Левая часть этого уравнения представляет полный дифференциал некоторой функции U(X,Y), так что
. Следовательно, уравнение является уравнением в полных дифференциалах. Левая часть этого уравнения представляет полный дифференциал некоторой функции U(X,Y), так что
![]() и
и ![]() . Проинтегрируем первое уравнение по X:
. Проинтегрируем первое уравнение по X:
![]() . Таким образом,
. Таким образом, ![]() , где φ(Y) – произвольная функция. Найдём эту функцию, пользуясь вторым уравнением. С одной стороны
, где φ(Y) – произвольная функция. Найдём эту функцию, пользуясь вторым уравнением. С одной стороны ![]() . С другой стороны,
. С другой стороны, ![]() . Приравнивая эти выражения, получим:
. Приравнивая эти выражения, получим: ![]() . Отсюда,
. Отсюда, ![]() . Согласно уравнению, DU=0. Решением уравнения будет U(x, y)=C. В данном случае
. Согласно уравнению, DU=0. Решением уравнения будет U(x, y)=C. В данном случае ![]() . Ответ:
. Ответ: ![]() .
.
5. ![]() Уравнение второго порядка, допускающее понижение порядка. В уравнении отсутствует искомая функция Y. Сделаем замену
Уравнение второго порядка, допускающее понижение порядка. В уравнении отсутствует искомая функция Y. Сделаем замену ![]() . Тогда
. Тогда ![]() . Получим линейное уравнение первого порядка:
. Получим линейное уравнение первого порядка: ![]() . Решаем сначала однородное уравнение:
. Решаем сначала однородное уравнение: ![]() . Далее решаем неоднородное уравнение методом вариации произвольной постоянной:
. Далее решаем неоднородное уравнение методом вариации произвольной постоянной: ![]()
![]() . Таким образом,
. Таким образом, ![]() . Определим постоянную C2, пользуясь начальным условием
. Определим постоянную C2, пользуясь начальным условием ![]() :
: ![]() . Следовательно,
. Следовательно, ![]() . Тогда
. Тогда ![]() . Определим C3, пользуясь вторым начальным условием
. Определим C3, пользуясь вторым начальным условием ![]() :
: ![]() . Окончательно,
. Окончательно, ![]() . Ответ:
. Ответ: ![]() .
.
6. ![]() Линейное неоднородное уравнение второго порядка. Решим уравнение методом вариации произвольных постоянных. Найдём сначала решение однородного уравнения
Линейное неоднородное уравнение второго порядка. Решим уравнение методом вариации произвольных постоянных. Найдём сначала решение однородного уравнения ![]() . Характеристическое уравнение
. Характеристическое уравнение ![]() имеет два корня:
имеет два корня: ![]() . Получаем два частных решений:
. Получаем два частных решений: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Будем считать, что решение неоднородного уравнения имеет такую же структуру, но С1 и С2 являются функциями переменной Х:
. Будем считать, что решение неоднородного уравнения имеет такую же структуру, но С1 и С2 являются функциями переменной Х: ![]() . Тогда, в соответствии с методом вариации произвольных постоянных, неизвестные функции С1(Х) и С2(Х) определяются системой уравнений:
. Тогда, в соответствии с методом вариации произвольных постоянных, неизвестные функции С1(Х) и С2(Х) определяются системой уравнений: 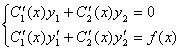 , где F(X) – правая часть неоднородного уравнения. В данном случае имеем систему:
, где F(X) – правая часть неоднородного уравнения. В данном случае имеем систему:  . Решим систему методом Крамера:
. Решим систему методом Крамера:  . Интегрируем:
. Интегрируем: ![]() . Следовательно, решением неоднородного уравнения будет
. Следовательно, решением неоднородного уравнения будет ![]() . Теперь можно вернуться к прежним обозначениям произвольных постоянных. Положим С1=С3 и С2=С4. Окончательно,
. Теперь можно вернуться к прежним обозначениям произвольных постоянных. Положим С1=С3 и С2=С4. Окончательно, ![]() .
.
Ответ: ![]() .
.
7. ![]() . Линейное неоднородное уравнение третьего порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение третьего порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет три корня:
имеет три корня: ![]() . Получаем три частных решения:
. Получаем три частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное решение неоднородного уравнения, исходя из структуры его правой части:
. Найдём частное решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Здесь множитель Х обусловлен тем, что корень характеристического уравнения R=0 совпадает с коэффициентом α в экспоненте EαX, «стоящей» в правой части уравнения (α=0). Найдём производные YЧн::
. Здесь множитель Х обусловлен тем, что корень характеристического уравнения R=0 совпадает с коэффициентом α в экспоненте EαX, «стоящей» в правой части уравнения (α=0). Найдём производные YЧн:: ![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение: ![]() . Отсюда находим:
. Отсюда находим: ![]()
![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() .
.
Ответ: ![]() .
.
8. ![]() . Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет два корня:
имеет два корня: ![]() . Получаем два частных решения:
. Получаем два частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное решение неоднородного уравнения, исходя из структуры его правой части:
. Найдём частное решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Найдём производные YЧн::
. Найдём производные YЧн:: ![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение:
![]() . Отсюда находим
. Отсюда находим ![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() . Воспользуемся начальными условиями:
. Воспользуемся начальными условиями: ![]() . По первому условию
. По первому условию ![]() . Найдём
. Найдём ![]() . Тогда, по второму условию,
. Тогда, по второму условию, ![]() . Решая систему
. Решая систему  , находим:
, находим: ![]() . Частное решение уравнения будет
. Частное решение уравнения будет ![]() . Ответ:
. Ответ: ![]() .
.
9. ![]() . Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет два корня:
имеет два корня: ![]() . Получаем два частных решения:
. Получаем два частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное решение неоднородного уравнения, исходя из структуры его правой части:
. Найдём частное решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Найдём производные yчн::
. Найдём производные yчн::
![]()
![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение:
![]()
![]() . Сокращая на
. Сокращая на ![]() и приравнивая коэффициенты при одинаковых функциях в левой и правой частях равенства, находим
и приравнивая коэффициенты при одинаковых функциях в левой и правой частях равенства, находим ![]() . Или
. Или![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() .
.
Ответ: ![]() .
.
10. Решить систему линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами ![]() , где
, где 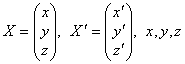 - функции от T, M – матрица коэффициентов, при начальных условиях
- функции от T, M – матрица коэффициентов, при начальных условиях ![]() :
:
 .
.
Запишем систему по исходным данным:
 . Ищем решение в виде
. Ищем решение в виде 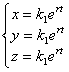 . Тогда
. Тогда 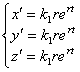 . Подставляя это в систему, получим систему алгебраических уравнений, которая определяет неизвестные коэффициенты
. Подставляя это в систему, получим систему алгебраических уравнений, которая определяет неизвестные коэффициенты ![]() :
:  . Приравнивая определитель системы к нулю, получим характеристическое уравнение исходной системы:
. Приравнивая определитель системы к нулю, получим характеристическое уравнение исходной системы:  . Раскроем определитель:
. Раскроем определитель: ![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . При
. При ![]() получим систему:
получим систему:  . Отбросим второе уравнение, как линейно зависимое. Получим
. Отбросим второе уравнение, как линейно зависимое. Получим ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Получили первое частное решение:
. Получили первое частное решение: ![]() . При
. При ![]() получим систему:
получим систему:  . Отбросим второе уравнение, как линейно зависимое. Получим
. Отбросим второе уравнение, как линейно зависимое. Получим ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Получили второе частное решение:
. Получили второе частное решение: ![]() .
.
При ![]() получим систему:
получим систему:  . Отбросим второе уравнение, как линейно зависимое. Получим
. Отбросим второе уравнение, как линейно зависимое. Получим ![]() . Система имеет решения только при
. Система имеет решения только при ![]() . Тогда
. Тогда ![]() . Получили третье частное решение:
. Получили третье частное решение: ![]() . Общее решение записывается как линейная комбинация частных решений:
. Общее решение записывается как линейная комбинация частных решений:  .
.
Найдём произвольные постоянные, пользуясь начальными условиями. При T=0 получим систему:  . Исключим С1, пользуясь третьим уравнением. Получим:
. Исключим С1, пользуясь третьим уравнением. Получим:  . Следовательно,
. Следовательно, ![]() . Таким образом, частное решение системы следующее:
. Таким образом, частное решение системы следующее:  . Ответ:
. Ответ:  .
.
11. Найдите уравнение кривой, проходящей через точку M(2; 2) и обладающей свойством, что отрезок любой касательной, заключённой между точкой касания и осью абсцисс, делит ось ординат пополам. (Непонятная формулировка. Решение приводится в предположении, что отрезок делится осью ординат пополам)
Уравнение касательной к кривой ![]() в точке
в точке ![]() имеет вид
имеет вид ![]() . Найдём точку пересечения касательной с осями координат. Положим Y=0. Тогда
. Найдём точку пересечения касательной с осями координат. Положим Y=0. Тогда ![]() или
или ![]() . Точка М1
. Точка М1 ![]() является точкой пересечения оси ОХ. Положим X=0. Тогда
является точкой пересечения оси ОХ. Положим X=0. Тогда ![]() или
или ![]() . Точка М2
. Точка М2![]() является точкой пересечения оси ОУ. Так как в точке M2 отрезок M1M0 делится пополам, то её координаты являются средними арифметическими координат точек M1 и M0. Следовательно, ордината точки M2 равна
является точкой пересечения оси ОУ. Так как в точке M2 отрезок M1M0 делится пополам, то её координаты являются средними арифметическими координат точек M1 и M0. Следовательно, ордината точки M2 равна ![]() . С другой стороны, эта ордината равна
. С другой стороны, эта ордината равна ![]() . Получили уравнение:
. Получили уравнение: ![]() Это равенство справедливо для любой точки
Это равенство справедливо для любой точки ![]() . Заменим эту точку произвольной точкой
. Заменим эту точку произвольной точкой ![]() , лежащей на кривой
, лежащей на кривой ![]() . Получим:
. Получим: ![]() . Разделяем переменные:
. Разделяем переменные: ![]() . Интегрируем:
. Интегрируем: ![]() или
или ![]() . Решение
. Решение ![]() отбросим, так как это прямая линия. Найдём C в решении
отбросим, так как это прямая линия. Найдём C в решении ![]() , учитывая, что кривая проходит через точку М(2, 2):
, учитывая, что кривая проходит через точку М(2, 2): ![]() . Таким образом,
. Таким образом, ![]() . Или
. Или  Ответ:
Ответ:  .
.
12. Из эксперимента известно, что скорость остывания(или нагрева) тела пропорциональна разности температур тела и окружающей среды. Пусть за 10 минут тело охладилось от1000 до 600. Температура окружающего воздуха поддерживается равной 200. Когда тело остынет до 250?
Пусть температура тела к моменту времени T равна T(T). Тогда, по условию задачи, ![]() , где K – некоторый коэффициент. Решим уравнение:
, где K – некоторый коэффициент. Решим уравнение: ![]()
![]() В момент
В момент ![]() температура была равна 1000. Тогда
температура была равна 1000. Тогда ![]() . Известно, что за 10 температура изменилась до 600, т. е.
. Известно, что за 10 температура изменилась до 600, т. е. ![]() . Отсюда находим:
. Отсюда находим: ![]() . Тогда
. Тогда ![]() . Если
. Если ![]() , то
, то ![]() .
.
Ответ: ![]() мин.
мин.
| < Предыдущая | Следующая > |
|---|