Теория вероятности (18 задач)

1 вариант.

1. Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число кратно 5?

В нашем случае элементарным исходом является выбор одного числа от до

$\omega=\left\{1,2,3,...,20}ight\}$ - пространство элементарных исходов.

- количество всех элементарных исходов.

Итак, все элементарные исходы равновозможны, т. к. натуральное число выбирается наудачу и пространство элементарных исходов конечно, следовательно, эксперимент, описанный в задаче, удовлетворяет классическому определению вероятности.

- выбранное число является делителем

- множество благоприятствующих исходов.

- количество всех благоприятствующих исходов.

- искомая вероятность.

Ответ:

2. В урне три белых и пять черных шаров. Наудачу вынимают два шара. Какова вероятность того, что эти шары разных цветов?

Решение

Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 8 шаров вынуть два, т. е. числу сочетаний из 8 элементов по 2:

Число благоприятствующих исходов (числу способов, которыми можно из 3 белых шаров вынуть один и из 5 чёрных шаровы вынуть один):

Следовательно, искомая вероятность

Ответ:

3. Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0,7. Для второго станка эта вероятность равна 0,8. На первом станке изготовлены всего 2 детали, на втором – 3. Найти вероятность того, что все детали первосортные.

Решение

Так как изготовление деталей на станках независимые события. То, по теореме умножения вероятностей независимых событий, искомая вероятность равна

Ответ:

4. В тире имеется 5 винтовок, вероятности попадания в цель из которых равны соответственно 0.5, 0.6, 0,7, 0,8 и 0,9. Определить вероятность попадания из взятой наугад винтовки.

Решение

Определим гипотезы:

Hi = {выбрана i-тая винтовка} i = 1, 2, 3, 4, 5.

A={попадание в мишень с одного выстрела}

A|Hi ={попадание в мишень из i-той винтовки}

Тогда их вероятности, по условию,

По формуле полной вероятности

Ответ:

5. 30% изделий некоторого предприятия – продукция высшего сорта. Приобретено 4 изделия этого предприятия. Какова вероятность того, что 2 из них высшего сорта?

Решение

Используем схему Бернулли. Здесь n= 4, m=2, p = 0,3, q =1-0,3= 0,7. Тогда по формуле

Вероятность того, что 2 изделия из 4 будут высшего сорта:

Ответ:

6. Пусть n – число независимых испытаний, р – вероятность появления события А в отдельном испытании, k – число наступлений события А за n испытаний:

А) , . Найти

Б) Найти , если ,

Решение

а) Так как n = 600 – велико, то в данном случае применяем локальную формулу Лапласа:

, где .

По условию задачи , , , .

Вычислим .

По таблице находим .

Теперь вычислим искомую вероятность

б) Вероятность того, что отклонение частости события от вероятности при n независимых испытаниях не превышает заданного , находится по формуле

Тогда, по условию

Имеем

Используем таблицу значений функции Лапласа

Отвте: ,

7. Случайная величина Х распределена по закону Коши: . Найьти коэффициент а, функцию распределения , вероятность попадания с. в. Х на интервал . Существует ли для с. в. Х числовые характеристики МХ и ДХ?

Решение

Найдём значение параметра а:

Тогда

Найдём функцию распределения

Найдём вероятность попадания с. в. Х на интервал

Посчитаем математическое ожидание и дисперсию:

Следовательно, для данной случайной величины не существуют ни М(Х) ни Д(Х)

8. Изделия испытываются на надёжность. Вероятность выхода из строя за время испытания для каждого изделия равна 0,9. Испытания заканчиваются после первого же изделия, не выдержавшего испытания. Найти математическое ожидание числа испытаний.

Решение

$\xi$ - число испытаний.

- вероятность того, что изделие выдержало испытание.

Тогда получим ряд распределения

Это геометрическое распределение

Найдём - математическое ожидание случайной величины , имеющей геометрическое распределение

= (сходится так как $0\textless q\textless 1$ )

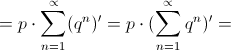
$=p\cdot \sum_{n=1}^{\propto }(q^{n})'=p\cdot (\sum_{n=1}^{\propto }q^{n})'=$ $=p\cdot (\frac{q}{1-q})'=p\cdot \frac{1-q+q}{(1-q)^2}=\frac{p}{(1-q)^2}=\frac{p}{p^2}=\frac{1}{p}$

В нашем случае р=0,9, следовательно

Ответ:

9. Найти коэффициент корреляции двумерной случайной величины (Х, Y), заданной матрицей:

X\y	1	2
-1	0.15	0.1
0	0.15	0.05
1	0.32	0.23

Решение

События (X=xi, Y=yj) образуют полную группу событий, поэтому сумма всех вероятностей pij(i=1,2...,n, j=1,2..,m), указанных в таблице, равна 1.

1. Зависимость случайных величин X и Y.

Находим ряды распределения X и Y.

Пользуясь формулой ∑P(xi, yj) = pi (j=1..n), находим ряд распределения X.

X	-1	0	1
P	0.25	0.2	0.55	∑Pi = 1

Математическое ожидание M[X]. M[x] = (-1)*0.25 + 0*0.2 + 1*0.55 = 0.3

Дисперсия D[X]. D[X] = 12*0.25 + 02*0.2 + 12*0.55 - 0.32 = 0.71

Среднее квадратическое отклонение σ(x).

Пользуясь формулой ∑P(xi, yj) = qj (i=1..m), находим ряд распределения Y.

Y	1	2
P	0.62	0.38	∑Pi = 1

Математическое ожидание M[Y]. M[y] = 1*0.62 + 2*0.38 = 1.38

Дисперсия D[Y]. D[Y] = 12*0.62 + 22*0.38 - 1.382 = 0.24

Среднее квадратическое отклонение σ(y).

Поскольку, P(X=-1,Y=1) = 0.15≠0.25•0.62, то случайные величины X и Y зависимы.

Ковариация. cov(X, Y) = M[X•Y] - M[X]•M[Y]

Cov(X, Y)=1•(-1)•0.15+2•(-1)•0.1+1•0•0.15+2•0•0.05+1•1•0.32+2•1•0.23-0.3•1.38=0.016

Если случайные величины независимы, то их ковариации равна нулю. В нашем случае cov(X, Y) ≠ 0.

Коэффициент корреляции.

Ответ:

1. Брошены 3 монеты. Найти вероятность того, что выпадут 2 «герба».

Решение

В нашем случае элементарным исходом является выпадение одной из возможных комбинаций. Обозначим «г»-выпадение герба на монете, «р» - выпадение решки на монете. Тогда возможны ситуации:

Ггг, ргг, грг, ррг, ррр, ргр, ггр, грр

- пространство элементарных исходов.

N=8 - количество всех элементарных исходов.

Итак, все элементарные исходы равновозможны, следовательно эксперимент, описанный в задаче, удовлетворяет классическому определению вероятности.

- выпало 2 герба

- множество благоприятствующих исходов.

- количество всех благоприятствующих исходов.

- искомая вероятность.

Ответ:

2. Из 10 карточек с буквами А, Д, А, Б, А, Д, В, Г, Д, А наудачу выбираются 3. Какова вероятность того, что из этих карточек можно сложить слово «два»?

Решение

Число всевозможных исходов-количество способов вытянуть 3 карточки из 10.

A = {из отобранных карточек можно составить слово «два»}

Число благоприятных исходов-количество способов вытянуть 3 буквы из которых можно составить слово «раз»:

M=3*1*4=12 – по теореме умножения вероятностей независимых событий.

Используем формулу классического определения вероятности:

Ответ:

3. Стрелок стреляет 3 раза по удаляющейся цели. Вероятность попадания при первом выстреле – 0,8, при втором – 0,7 и при третьем – 0,6. Какова вероятность хотя бы одного попадания?

Решение

Вероятность не попасть при первом выстреле 1-0,8=0,2, вероятность не попасть при втором выстреле 1-0,7=0,3, вероятность не попасть при третьем выстреле 1-0,6=0,4.

По теореме об умножении вероятностей независимых событий, вероятность не попасть при трёх выстрелах 0,2*0,3*0,4=0,024.

Значит вероятность хотя бы одного попадания (противоположное событие): 1-0,024=0,976.

Ответ: 0,976.

4. 60% школьников – девочки. 80% девочек и 75% мальчиков имеют билеты в театр. В учительскую принесли потерянный кем-то билет. Какова вероятность того, что этот билет принадлежит девочке?

Решение

Определим гипотезы:

H1 = билет потеряла девочки

H2 = билет потерял мальчик

A={билет был потерян}

A|H1 ={был потерян билет, и он принадлежал девочке}

A|H2 ={был потерян билет, и он принадлежал мальчику}

Тогда их вероятности, по условию,

По формуле Байеса

Ответ:

5. Изделия некоторого предприятия содержат 5% брака. Найти вероятность того, что среди 5 взятых наудачу изделий будут 2 бракованных.

Решение

Используем схему Бернулли.

Здесь n=5, m=2, p=0,05, q=1-0,05=0,95. Тогда по формуле

Вероятность того, что 2 изделия из 5 будут бракованные:

Ответ:

А) , . Найти

Б) Найти , если ,

Решение

а) Так как n = 600 – велико, то в данном случае применяем интегральную формулу Лапласа:

= Ф(х´´) – Ф(х´), где х´ = ; х´´ = ,

т. к. , , , , имеем

Х´ = ; х´´ = .

По таблицам найдем значения Ф(-1)=-Ф(1)=-0,34134

Тогда искомая вероятность будет

= Ф(1) – Ф(-1) =2Ф(1)= 2*0,34134=0,68268

Тогда, по условию

Имеем

Используем таблицу значений функции Лапласа

Ответ: =0,68268,

7. Производятся 20 независимых испытаний, в каждом из которых вероятность появления успеха равна 0,2. Найти дисперсию числа появлений успеха в этих испытаниях.

Решение

Случайная величина X - число появлений успеха при 20 независимых испытаниях.
n = 20 - количество независимых испытаний

P = 0.2 - вероятность успеха при одном испытании

Q = 1 - p = 1 - 0.2 = 0.8

Случайная величина X имеет распределение Бернулли с параметрами

N = 20 и p = 0.2

D(X) = npq = 20*(0.2)*(0.8) = 3.2

Ответ: D(X)=3.2

8. Случайная величина Х равномерно распределена на . Построить графики и . Найти , если с. в.