Элементы теории множеств и теории нечётких множеств
Задание 1. На универсальном множестве 
заданы нечёткие множества 
и 
:
Найти нечёткие множества 
, 
.
Решение. По определению объединением нечётких множеств и называется наименьшее нечёткое множество , которое содержит как , так и , и 
Тогда
.
Пересечением нечётких множеств и называется наибольшее нечёткое множество 
, содержащееся одновременно в и , и 
Следовательно,
.
Разностью нечётких множеств и называется нечёткое множество, которое определяется соотношением 
. Определим сначала множество 
:
.
Так как , то
.
Ответ: ,
,
.
Задание 2. На универсальном множестве заданы нечёткие множества и :
Найти 
.
Решение. Нечёткое множество называется дизъюнктивной суммой нечётких множеств и и определяется соотношением
.
Найдём множества 
и :
,
.
Пользуясь определением операции пересечения нечётких множеств, найдём нечёткие множества 
и 
:
.
Окончательно получаем, что
.
Ответ: .
Задание 3. На универсальном множестве заданы нечёткие множества
И 
.
Проверить, какое из включений истинно: 1) 
; 2) 
.
Решение.
1) Нечёткое множество содержит нечёткое множество , если 
. Данное условие не выполняется.
2) Нечёткое множество содержит нечёткое множество , если 
. Данное условие выполняется.
Ответ: 1) нет; 2) да.
Задание 4. Найти для заданного нечёткого множества 
ближайшее к нему обычное множество 
, евклидово расстояние и расстояние Хэмминга между этими множествами, а также относительные величины этих расстояний.
Решение. Функция принадлежности элемента 
универсального множества 
к множеству рассчитывается по правилу:
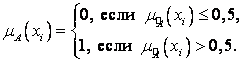
Очевидно, 
.
Вычислим евклидово расстояние и расстояние Хэмминга между множествами и :
,
,
Тогда относительное евклидово расстояние и относительное расстояние Хэмминга, соответственно, равны:
и 
.
Ответ: ;
; 
; 
; 
.
Задание 5. На универсальном множестве заданы нечёткие множества
и
.
Найти нечёткие множества: 1) ; 2) ; 3) 
; 4) ; 5) найти евклидово расстояние и расстояние Хэмминга между множествами и ; 6) найти относительные евклидово и Хэмминга расстояния между этими множествами.
Решение.
1) Нечёткое множество :
.
2) Нечёткое множество :
.
3) Нечёткое множество :
.
4) По определению . Тогда
.
5) Евклидово расстояние между множествами и :
.
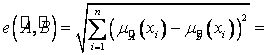
Расстояние Хэмминга между множествами и :
.
6) Относительное евклидово расстояние:
.
Относительное расстояние Хэмминга:
.
Ответ:
1) ;
2) ;
3) ;
4) ;
5) 
, 
;
6) 
, 
.
| < Предыдущая | Следующая > |
|---|