76. Задача Неймана (вторая краевая задача)

Опр: Пусть - односвязная жорданова область с гладкой границей , на которой функция непрерывна. Задача Неймана: Найти гармоническую функцию в , которая непрерывно дифференцируема вплоть до границы (то есть частные производные и непрерывны в ) и такую, что , где - внешняя нормаль к в точке .

Примечание: Так как не определена вне области , то, используя тот факт, что градиент непрерывен вплоть до границы, производную по нормали на границе можно понимать, как скалярное произведение: .

Утверждение: Для существования решения задачи Неймана необходимо, чтобы .

Доказательство: Пусть - решение задачи Неймана, тогда в силу того, что - односвязная, - гармонически сопряженная функция для и функция является аналитической в . Из условия задачи и условия Коши-Римана, получаем: , где - производная по направлению касательной к в точке в положительном направлении обхода (см. рисунок). Тогда получаем: . Утверждение доказано.

Формула для решения задачи Неймана в круге (без доказательства): Если - единичный круг, то при выполнении необходимого условия , или верна Формула Дини: .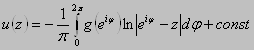

< Предыдущая		Следующая >