14.1. Понятие производной, ее геометрический и физический смысл
Касательной к линии В точке
В точке Называется прямая
Называется прямая - предельное
- предельное
Положение (рис. 14.1) секущей Когда точка
Когда точка Стремится к
Стремится к Вдоль дан
Вдоль дан
Ной линии (т. е. угол Стремится к нулю) произвольным образом.
Стремится к нулю) произвольным образом.
Производной функции В точке
В точке Называется предел отношения при
Называется предел отношения при
Ращения этой функции к приращению аргумента, когда последнее стремится к нулю.
Производную функции В точке
В точке Обозначают символом
Обозначают символом
(читается: «эф штрих от ») или
») или . Следовательно, по определению
. Следовательно, по определению
 (14.1)
(14.1)
Употребляются и другие обозначения:
 если
если

Термин «производная» (а также «вторая производная») ввел Ж. Лагранж (1797), он же предложил обозначения  (1770, 1779). Обозначение
(1770, 1779). Обозначение Впервые встречается
Впервые встречается
Лейбница (1675).
Геометрический смысл производной. Производная функции при
при Равна угловому коэффициенту касательной к графику данной функции
Равна угловому коэффициенту касательной к графику данной функции
В точке Т. е.
Т. е.
Где - угол наклона касательной к оси
- угол наклона касательной к оси Прямоугольной декартовой системы координат (рис. 14.2).
Прямоугольной декартовой системы координат (рис. 14.2).
Уравнение касательной к линии В точке
В точке Принимает вид
Принимает вид

























Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если /(х0)* О, то уравнение нормали к линии у = /(х) в точке М0(х0, у0) запишется так:
У~Уо^~~^т~~т(х~хо)- (14-4)
/'(*<>)
Физический смысл производной. Если х — /(/) - закон прямолинейного движения точки, то х' = /'(О — скорость этого движения в момент времени I.
Быстрота протекания физических, химических и других процессов выражается с помощью производной.
Если отношение Ду/Дх при х—»х0 имеет
Предел справа (или слева), то он называется производной справа (соответственно производной слева). Такие пределы называются односторонними производными.
Односторонние производные функции /(х) в точке х0 обозначается соответственно символами /Дх0), /+'(х0):
Г,, ч /(х0+Дх)-/(х0)
]Лхо)= 1™ ¦ --———- - производная слева;
Дг-»-0 Дх
. .. /(х0+Дх)-/(х0)
/Лхо)= Нт - —у--—- —— - производная справа.
ДХ-++0 Дх
Очевидно, функция /(х), определенная в некоторой окрестности точки х0, имеет производную /'(х0) тогда и только тогда, когда односторонние производные /_'(х0), /+'(х0) существуют и равны между собой, причем /_'(х0)= /+'(х0) = /'(х0).
Если для некоторого значения х выполняется одно из условий
Нт = + Нт — = - оо,
Дг-»0 Дх Дх—>0 Дх
То говорят, что в точке х существует бесконечная производная, равная соответственно +<*>,
Геометрическое истолкование производной как углового коэффициента касательной к графику распространяется и на этот случай: касательная в данном случае параллельна оси Оу (рис. 14.3, а - Ь).
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке. Если промежуток является замкнутым, то на концах его имеются односторонние производные.
Операция нахождения производной называется дифференцированием.
Зависимость между непрерывностью и дифференцируемостью функции выражается следующей теоремой.
Теорема 14.1. Если функция Дифференцируема в данной точке,
Дифференцируема в данной точке,
То она и непрерывна в ней.
Замечание. Обратное утверждение не всегда верно. Например, функция Непрерывна в точке
Непрерывна в точке Но не является дифферен
Но не является дифферен
Цируемой в ней.

Рис. 14.3
Пример 14.1. Записать уравнение касательной к линии
 В точке
В точке
Так как То в
То в
Соответствии с уравнением (14.3) получаем Или
Или
Пример 14.2. В какой точке касательная к линии Па
Па
Раллельна прямой
Данная прямая имеет угловой коэффициент Поскольку
Поскольку
 То в силу равенства (14.2) имеем
То в силу равенства (14.2) имеем Или
Или Откуда
Откуда
 Находим
Находим Сле
Сле
Довательно, получили две точки:
Пример 14.3. Записать уравнение нормали к линии
В точке
Так как
 То уравнение (14.4) принимает вид
То уравнение (14.4) принимает вид Или
Или 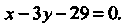
| < Предыдущая | Следующая > |
|---|
