11.7. Упрощение уравнений фигур второго порядка на плоскости
Фигурой второго порядка на плоскости называется множество точек этой плоскости, декартовы координаты которых удовлетворяют уравнению второй степени
Где Одновременно в нуль не обращаются. Отметим, что это множест
Одновременно в нуль не обращаются. Отметим, что это множест
Во, в частности, может состоять из единственной точки или оказаться пустым.
Первые три члена левой части уравнения (11.12) образуют квадратичную форму двух переменных
 (11.13)
(11.13)
С симметрической матрицей

(11.14)
По теореме 11.10 эту квадратичную форму ортогональным преобразованием можно привести к каноническому виду
 (11.15)
(11.15)
С матрицей

(11.16)
Где - характеристические числа матрицы
- характеристические числа матрицы , т. е. корни характеристиче
, т. е. корни характеристиче
Ского уравнения матрицы :
:

При этом ортогональном преобразовании уравнение (11.12) примет ввд
(11.17)
 (11.18)
(11.18)
Это уравнение можно привести к каноническому виду путем выделения в левой части полных квадратов.
Фигуру второго порядка, определяемую уравнением (11.12), называют центральной, если И нецентральной, когда
И нецентральной, когда
Отметим, что при ортогональном преобразовании переменных определитель матрицы квадратичной формы не меняется, т. е. Так как
Так как
 (см. (11.16)), то
(см. (11.16)), то
 (11.19)
(11.19)
Пусть уравнение (11.18) определяет центральную фигуру, т. е. Здесь
Здесь
Возможны два случая: (числа
(числа Одного знака), фигура называ
Одного знака), фигура называ
Ется фигурой эллиптического типа; (числа
(числа Имеют разные
Имеют разные
Знаки), фигура называется фигурой гиперболического типа.
Если То уравнение (11.18), выделив в его левой части полные квадра
То уравнение (11.18), выделив в его левой части полные квадра
Ты, можно привести к виду

Или
Где
Формулы (11.21) выражают зависимость между координатами при параллельном переносе координатных осей в точку
при параллельном переносе координатных осей в точку
В случае Уравнение (11.20) приводится к одному из канонических видов
Уравнение (11.20) приводится к одному из канонических видов
(11.23)
 (11.24)
(11.24)
В зависимости от знаков И
И
Уравнение (11.22) определяет эллипс, уравнению (11.23) не удовлетворяют координаты ни одной точки плоскости, уравнению (11.24) удовлетворяют координаты одной точки
В случае Уравнение (11.20) приводится к одному из канонических видов
Уравнение (11.20) приводится к одному из канонических видов
(11.25)
(11.26)  (11.27)
(11.27)
В зависимости от знаков
Уравнение (11.25) определяет гиперболу с действительной осью , уравнение (11.26) — гиперболу с действительной осью
, уравнение (11.26) — гиперболу с действительной осью Уравнение (11.27) - пару пересекающихся прямых, так как оно распадается на два уравнения
Уравнение (11.27) - пару пересекающихся прямых, так как оно распадается на два уравнения
 Или
Или
Обратимся к нецентральным фигурам, т. е. к случаю когда В силу
В силу
(11.19) из равенства Следует, что
Следует, что Последнее равенство означа
Последнее равенство означа
Ет, что одно из чисел Равно нулю (оба числа
Равно нулю (оба числа В нуль обратиться не
В нуль обратиться не
Могут, так как это означало бы, что квадратичная форма (11.15) является вырожденной, чего быть не может, поскольку ). Если
). Если То уравнение (11.18) можно привести к виду
То уравнение (11.18) можно привести к виду И записать так:
И записать так:
 (11.28)
(11.28)
Осуществим параллельный перенос репера На вектор
На вектор
 Получим новую систему координат
Получим новую систему координат , причем
, причем Определяются формулами (11.21). Уравнение (11.28) приведем к виду
Определяются формулами (11.21). Уравнение (11.28) приведем к виду
 (11.29)
(11.29)
Уравнение (11.29) определяет параболу с осью
Если в уравнении (11.18) То, выделив полный квадрат, его
То, выделив полный квадрат, его
Можно записать так:
 (11.30)
(11.30)
Осуществив параллельный перенос репера На вектор
На вектор
Т. е. выполнив преобразование Получим новую систему коор
Получим новую систему коор
Динат О, АТ, в которой уравнение (11.30) принимает один из видов:
 (11.31)
(11.31)
В зависимости от соотношения знаков чиЬел И
И
 Пер
Пер
Вое из уравнений (11.31) определяет пару параллельных прямых второму уравнению не удовлетворяют координаты ни одной точки плоскости, третье уравнение определяет пару совпавших прямых
второму уравнению не удовлетворяют координаты ни одной точки плоскости, третье уравнение определяет пару совпавших прямых
Операция перехода от уравнения (11.12) к уравнению (11.18) называется отнесением фигуры к главным осям. Новые оси координат параллельны осям симметрии фигуры. Главными направлениями фигуры, заданной уравнением (11.12), называют направления ортогональных собственных векторов матрицы квадратичной формы, соответствующей этому уравнению.
Из теорем п. 11.6 следует, что существует декартова прямоугольная система координат, в которой уравнение (11.12) принимает канонический вид. Чтобы выбрать эту систему координат, необходимо сделать следующее.
1. Найти ортогональное преобразование, приводящее к каноническому виду квадратичную форму, соответствующую данному уравнению.
2. С помощью этого преобразования определить главные направления фигуры, т. е. векторы - ортонормированные собственные векторы матрицы указанной квадратичной формы.
- ортонормированные собственные векторы матрицы указанной квадратичной формы.
3. Найти уравнение фигуры в репере
4. Выделить полные квадраты в полученном уравнении.
5. Совершить параллельный перенос системы На соответствующий вектор
На соответствующий вектор И составить каноническое уравнение фигуры в репере
И составить каноническое уравнение фигуры в репере
Пример 11.4. Какую линию на плоскости определяет уравнение

С помощью теории квадратичных форм приведем это уравнение к каноническому виду. Левая часть уравнения - квадратичная форма
 Которая с точность до обозначений переменных
Которая с точность до обозначений переменных
 ) (см. п. 11.6, пример 11.3) приведена к каноническому
) (см. п. 11.6, пример 11.3) приведена к каноническому
Виду Посредством ортогонального преобразования
Посредством ортогонального преобразования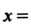

Это преобразование данное уравнение переводит в уравнение 
 Полученное уравнение определяет эллипс с полуосями
Полученное уравнение определяет эллипс с полуосями
| < Предыдущая | Следующая > |
|---|


