07.5.1. Геометрические приложения определенного интеграла. Площадь плоской фигуры
Рассмотрим на плоскости Оху фигуру, ограниченную графиком непрерывной и положительной функции F(X) на отрезке [А, B], отрезком [А, B] и вертикальными прямыми Х = А и Х = b (рис. 7.2). Эту фигуру будем называть Криволинейной трапецией.

Величина площади криволинейной трапеции равна определенному интегралу от функции f(x) на отрезке [а, b]:
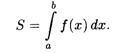
Если фигура ограничена сверху и снизу неотрицательными функциями F(X) и G(х) соответственно, непрерывными на отрезке [А, B], то площадь S криволинейной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху графиками F(X) и G(х):
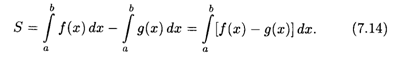
Рассмотрим задачи на вычисление площадей фигур.
Пример 1. Найти площадь фигуры, ограниченной графиком функции У = ln X ≥ 0, осью Ох и прямой Х = 2.
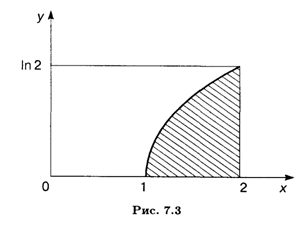
Решение. Отрезок интегрирования: 1 ≤ Х ≤ 2 (рис. 7.3), так что искомая площадь согласно формуле (7.14) равна:
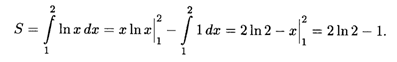
Пример 2. Найти площадь фигуры, ограниченной линиями У = ![]() , у = х2.
, у = х2.
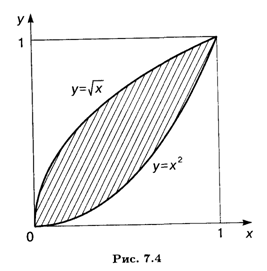
Решение. Вычислим абсциссы точек пересечения указанных кривых, для чего приравняем правые части этих уравнений: Х2 = ![]() . Корни этого уравнения суть X1 = 0, X2 = 1. Следовательно, площадь фигуры, ограниченной сверху функцией у =
. Корни этого уравнения суть X1 = 0, X2 = 1. Следовательно, площадь фигуры, ограниченной сверху функцией у = ![]() и снизу функцией У = X2 (рис. 7.4), дается определенным интегралом на отрезке [0,1]:
и снизу функцией У = X2 (рис. 7.4), дается определенным интегралом на отрезке [0,1]:
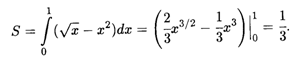
| < Предыдущая | Следующая > |
|---|