05.3.2. Выпуклость и точки перегиба графика функции
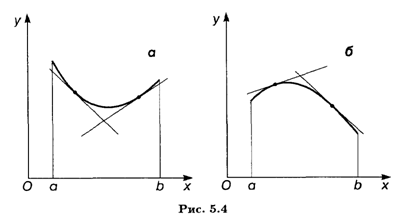
Определение 2. Будем говорить, что график функции Y = F(X) Имеет на интервале (А, B) Выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (А, B) (рис. 5.4).
Способ определения направления выпуклости графика функции дается теоремой, приведенной ниже без доказательства.
ТЕОРЕМА 5. Если функция у = f(х) имеет на интервале (а, b) вторую производную и F"(X) ≥ 0 (F"(X) ≤ 0) на (а, b), то график функции имеет на (а, b) выпуклость, направленную вниз (вверх).
Определение 3. Точка М(X0, F(X0)) называется Точкой перегиба графика функции У = F(X), если в точке М график имеет касательную и существует такая окрестность точки X0, в пределах которой график функции F(X) имеет разные направления выпуклости.
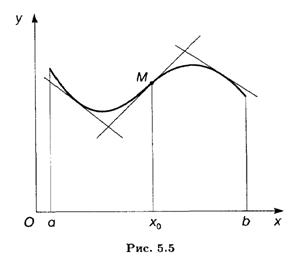
В точке перегиба касательная пересекает график функции, поскольку он переходит с одной стороны касательной на другую, т. е. "перегибается" через нее (рис. 5.5).
ТЕОРЕМА 6. (необходимое условие существования точки перегиба). Пусть график функции у = F(X) Имеет перегиб в точке M(X0, F(X0)) и функция f(x) имеет в точке x0 непрерывную вторую производную. Тогда
![]()
Отметим, что не всегда условие F"(X0) = 0 означает наличие точки перегиба на графике функции У = F(X). Например, график функции У = X2N (п > 1) не имеет перегиба в точке (0, 0), хотя при Х = 0 вторая производная равна нулю. Потому равенство (5.8) является только необходимым условием перегиба. Точки графика, для которых условие (5.8) выполнено, будем называть Критическими. В каждой такой точке необходимо исследовать дополнительно вопрос о наличии перегиба; здесь имеется полная аналогия с существованием экстремума функции.
ТЕОРЕМА 7 (достаточное условие существования точки перегиба). Пусть в некоторой окрестности точки x0 вторая производная функции у = f(x) имеет разные знаки слева и справа от x0. Тогда график у = F(X) имеет перегиб в точке М(x0, F(x0)).
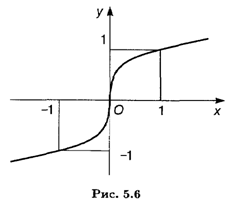
Теорема верна и для случая, когда F"(X) существует в некоторой окрестности точки X0 за исключением самой точки X0 и существует касательная к графику функции в точке М. Например, функция F(X) = X1/3 в точке Х = 0 имеет бесконечные производные; в точке O(0, 0) касательная совпадает с осью Оу. Однако график этой функции имеет перегиб в начале координат, поскольку вторая производная F"(X) = -2 /(9X5/3) имеет разные знаки слева и справа от точки Х = 0 (рис. 5.6). Рассмотрим примеры: найти точки перегиба и направления выпуклости графиков следующих функций.
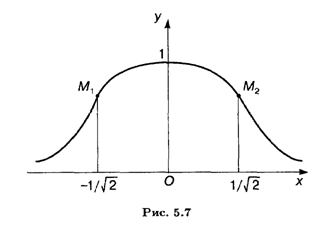
Пример 3. F(X) = ехр (-X2).
Решение. Последовательно находим F'(X)= -2X Exp(—X2), F"(X) = 2 exp (-x2)(2X2 — 1). Приравнивая вторую производную к нулю, получаем критические точки Х = ±1/![]() . Ввиду зависимости функции от Х2 достаточно исследовать точку X = l/
. Ввиду зависимости функции от Х2 достаточно исследовать точку X = l/![]() . Нетрудно видеть, что при переходе через эту точку слева направо F"(X) меняет знак с минуса на плюс. Следовательно, на левой ветви функции точка M1(-1 /
. Нетрудно видеть, что при переходе через эту точку слева направо F"(X) меняет знак с минуса на плюс. Следовательно, на левой ветви функции точка M1(-1 / ![]() , E-1/2) является точкой перегиба графика функции со сменой выпуклости вниз слева на выпуклость вверх справа (рис. 5.7). На правой ветви в точке перегиба М2(1/
, E-1/2) является точкой перегиба графика функции со сменой выпуклости вниз слева на выпуклость вверх справа (рис. 5.7). На правой ветви в точке перегиба М2(1/![]() , Е-1/2) графика функции имеет место смена выпуклости вверх слева на выпуклость вниз справа.
, Е-1/2) графика функции имеет место смена выпуклости вверх слева на выпуклость вниз справа.
Пример 4. F(X) = ln (Х2 – 2X + 2).
РHешение. Вторая производная равна ![]() . Приравнивая ее к нулю, получаем критические точки X1 = 0, X2 = 2. Несложный анализ квадратного трехчлена Х(2 — х), Стоящего в числителе второй производной и определяющего ее знак, показывает, что точка перегиба M1 (0, ln 2) графика функции меняет выпуклость вверх слева на выпуклость вниз справа; в другой точке перегиба М2 (2, ln2) выпуклость графика функции вниз слева меняется на выпуклость вверх справа.
. Приравнивая ее к нулю, получаем критические точки X1 = 0, X2 = 2. Несложный анализ квадратного трехчлена Х(2 — х), Стоящего в числителе второй производной и определяющего ее знак, показывает, что точка перегиба M1 (0, ln 2) графика функции меняет выпуклость вверх слева на выпуклость вниз справа; в другой точке перегиба М2 (2, ln2) выпуклость графика функции вниз слева меняется на выпуклость вверх справа.
| < Предыдущая | Следующая > |
|---|