45. Приближенные методы решения дифференциальных уравнений
Рассмотрим задачу Коши (5.3), (5.7) для дифференциального уравнения первого порядка: найти решение уравнения ![]() , удовлетворяющее условию
, удовлетворяющее условию ![]() . Пусть
. Пусть ![]() - решение поставленной задачи Коши. Подставив это решение в уравнение (5.3), получим тождество
- решение поставленной задачи Коши. Подставив это решение в уравнение (5.3), получим тождество ![]() . Интегрируя это тождество по
. Интегрируя это тождество по ![]() , получаем
, получаем
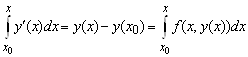 ,
,
Или, что то же самое,
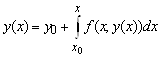 . (5.16)
. (5.16)
Таким образом, мы показали, что всякое решение задачи Коши (5.3), (5.7) есть решение интегрального уравнения (5.16). С другой стороны, если ![]() - дифференцируемое решение интегрального уравнения (5.16), то, дифференцируя (5.16) по
- дифференцируемое решение интегрального уравнения (5.16), то, дифференцируя (5.16) по ![]() , получаем, что
, получаем, что ![]() - решение задачи Коши (5.3), (5.7).
- решение задачи Коши (5.3), (5.7).
Решение интегрального уравнения (5.16) будем искать с помощью метода последовательных приближений. Положим
![]()
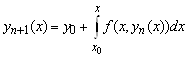 . (5.17)
. (5.17)
Оператор ![]() , отображающий метрическое пространство
, отображающий метрическое пространство ![]() в себя, называют сжимающим
в себя, называют сжимающим ![]() , если
, если ![]() , где
, где ![]() -расстояние в
-расстояние в ![]() ,
, ![]() .
.
Сжимающие операторы имеют неподвижную точку, то есть точку, которая оператором ![]() переводится в себя. Если линейное уравнение удаётся записать в виде
переводится в себя. Если линейное уравнение удаётся записать в виде ![]() в котором оператор
в котором оператор ![]() - сжимающий, то решение этого линейного уравнения можно найти с помощью последовательных приближений
- сжимающий, то решение этого линейного уравнения можно найти с помощью последовательных приближений ![]() , которые сходятся к решению уравнения
, которые сходятся к решению уравнения ![]() .
.
Таким образом, если оператор
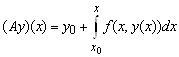 - (5.18)
- (5.18)
Сжимающий [12], то последовательные приближения (5.17) сходятся к решению интегрального уравнения (5.16), а, следовательно, и дифференциального уравнения ![]() , удовлетворяющему условию
, удовлетворяющему условию ![]() . Желающие могут познакомиться с доказательством сжимаемости оператора (5.18) в [12].
. Желающие могут познакомиться с доказательством сжимаемости оператора (5.18) в [12].
Пример. Найдём с помощью метода последовательных приближений решение уравнения ![]() , удовлетворяющее условию
, удовлетворяющее условию ![]() . Подставляя
. Подставляя ![]() в (5.17), получаем
в (5.17), получаем
![]()

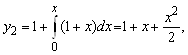 …,
…,
![]()
С другой стороны, решая исходную задачу Коши, имеем ![]() .
.
Таким образом, нами получено разложение функции ![]() в ряд Тейлора в нуле (ряд Маклорена).
в ряд Тейлора в нуле (ряд Маклорена).
Перейдём теперь к изложению численного метода Эйлера решения задачи Коши (5.3), (5.7). Разобьём отрезок ![]() , на котором мы ищем решение, на части точками
, на котором мы ищем решение, на части точками ![]()
![]() . Положим
. Положим ![]()
![]()
![]() . Так как по определению производной
. Так как по определению производной ![]() то, заменяя производную
то, заменяя производную ![]()
Конечной разностью ![]()
![]() в уравнении (5.3), получаем
в уравнении (5.3), получаем ![]() , или, что то же самое,
, или, что то же самое,
![]() . (5.19)
. (5.19)
Соотношение (5.19) является расчётной формулой метода Эйлера численного решения задачи Коши (5.3), (5.7). Вычислив ![]() получим таблицу значений решения в точках
получим таблицу значений решения в точках ![]() . Для оценки погрешности на одном шаге сетки в методе Эйлера разложим точное решение
. Для оценки погрешности на одном шаге сетки в методе Эйлера разложим точное решение ![]() По формуле Тейлора в окрестности точки
По формуле Тейлора в окрестности точки ![]() До членов второго порядка малости
До членов второго порядка малости
![]() .
.
Сравнивая с (5.19) видим, что погрешность формулы (5.19) на одном шаге равна ![]() . К сожалению, метод Эйлера накапливает ошибку от шага к шагу. Поэтому на практике пользуются либо модификациями метода Эйлера, например, методом прогноза и коррекции [14], либо другими методами, в частности методом Рунге-Кутта [14].
. К сожалению, метод Эйлера накапливает ошибку от шага к шагу. Поэтому на практике пользуются либо модификациями метода Эйлера, например, методом прогноза и коррекции [14], либо другими методами, в частности методом Рунге-Кутта [14].
| < Предыдущая | Следующая > |
|---|