Теория вероятности и математическая статистика 05
Блок «Теория вероятностей»
α = 1, β = 5
1. Устройство состоит из трех независимых элементов, работающих в течении времени t безотказно с вероятностями р1 = 0,94; р2 = 0,89; р3 = 0,75. Найти вероятность того, что за время t выйдет из строя:
А) только один элемент;
Б) хотя бы один элемент.
Предложим, что события:
А – за время выйдет из строя только один элемент;
В – за время выйдет из строя хотя бы один элемент.
Событие А можно представить следующим образом: ![]() . – первый работает, остальные два вышли из строя или первый и третий вышли из строя второй – работает или первый и второй элементы вышли из строя третий – работает.
. – первый работает, остальные два вышли из строя или первый и третий вышли из строя второй – работает или первый и второй элементы вышли из строя третий – работает.
Р1 = 0,94 – первый элемент работает; q1 = 1 - 0,94 = 0.06– первый элемент не работает;
Р2 = 0,89 – второй элемент работает; q2 = 1 - 0,89 = 0.11 - второй элемент не работает;
Р3 = 0,75 – третий элемент работает; q3 = 1 - 0,75 = 0.25 – третий элемент не работает;
Рассмотрим событие В. ![]() как противоположные события. Событие
как противоположные события. Событие ![]() можно представить следующим образом:
можно представить следующим образом: ![]() =
= ![]()
![]() ,
,
![]() .
.
Ответ: 1) ![]() 2)
2) ![]()
2. Плотность распределения непрерывной случайной величины имеет вид:
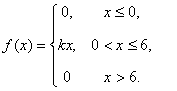
Найти:
А) параметр k и математическое ожидание M(x);
Б) Интегральную функцию распределения F(x) и вероятность события х > 2
А) Найдем параметр k из условия нормировки ![]() . Получаем:
. Получаем:
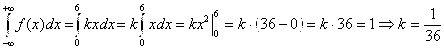
Тогда:
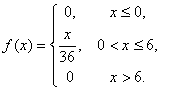
Вычислим математическое ожидание ![]()
,
Б) Воспользуемся формулой для нахождения функции распределения:
![]()
Если ![]() то
то ![]() , значит
, значит ![]() ;
;
Если ![]() то
то ![]() , значит
, значит
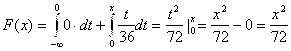
Если ![]() то
то ![]() , значит
, значит 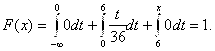
Таким образом, ![]() имеет вид:
имеет вид:
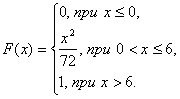
![]()
Ответ: а) 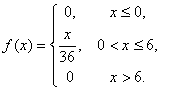 ; ; б)
; ; б) 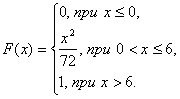 ;
; ![]()
Блок «Математическая статистика»
Выборка задана дискретным вариационным рядом

Требуется:
А) вычислить среднее выборочное;
Б) вычислить дисперсию;
В) вычислить среднее квадратичное отклонение;
Г) вычислить теоретические частоты (предполагая нормальное распределение генеральной совокупности);
Д) по критерию Пирсона проверить гипотезу о нормальном распределении совокупности при уровне значимости α = 0,05.
Решение
Введем вспомогательную переменную U
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]()
Г) ![]()
Тогда
![]()

Д) 
Так как α = 0,05; ![]() . По таблице находим:
. По таблице находим: ![]() Так как
Так как ![]() , то гипотеза о выбранном теоретическом нормальном законе согласуется с опытными данными.
, то гипотеза о выбранном теоретическом нормальном законе согласуется с опытными данными.
Домашнее задание по блоку «Математическая статистика».
Двумерная выборка результатов совместных измерений признаков Х и У задана корреляционной таблицей:
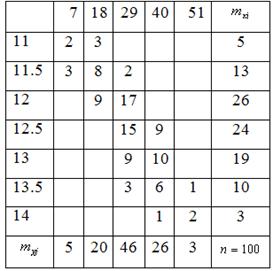
Найти: а) выборочный коэффициент корреляции;
Б) выборочное уравнение прямолинейной регрессии У на Х. построить график этого уравнения и точки корреляционного поля.
Решение
А) Уравнение линейной регрессии с y на x имеет вид:
![]()
Найдем необходимые числовые характеристики.
Выборочные средние:
![]()
![]()
Дисперсии:
![]()
![]()
Откуда получаем: σx = 0,72 и σy = 9,71, и ковариация:
Cov (х, у) = (11 × 7 × 2 + 11 × 18 × 3 + 11.5 × 7 × 3 + 11.5 × 18 × 8 + 11.5 × 29 × 2 + 12 × 18 × 9 + 12 × 29 × 17 + 12,5 × 29× 15 + 12,5 × 40 × 9 + 13 × 29 × 9+13 × 40 × 10+13.5 × 29 × 3+13.5 × 40 × 6+13.5 × 51 × 1+14 × 40 × 1+14 × 51 × 2) / 100 – 12,405 × 29,22 = =5,47
Определим коэффициент корреляции
![]()
Б) Запишем уравнения линий регрессии:
![]()
И вычисляя, получаем
![]()
Построим в одной системе данные точки и прямую регрессию.
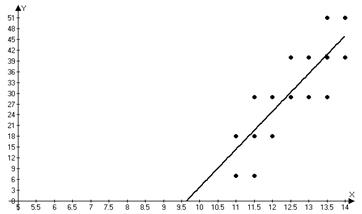
Рис 1
Домашнее задание по блоку «Теория вероятностей»
1. В урне содержится 8 черных и 8 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них:
А) ровно половина белых шаров;
Б) хотя бы один белый шар.
Решение
А) Пусть событие А – 2 шара белых.
По классическому определению вероятности.
![]()
![]()
![]() - благоприятных случаев
- благоприятных случаев
![]()
Б) хотя бы один белый шар.
Событию В (из вытянутых шаров хотя бы один белый) противоположно событие ![]() – ни один шар не белый, т. е. все шары черные:
– ни один шар не белый, т. е. все шары черные:
![]()
![]() - все шары черные
- все шары черные
![]()
![]() .
.
Ответ: а) ![]() б)
б) ![]()
2. В ящике 7 исправных и 7 неисправных ламп. К ним добавляют две лампы (все предположения об исправности этих ламп равновозможны). После этого из ящика случайным образом достают четыре лампы.
А) найти вероятность того, что все вынутые лампы исправны;
Б) найти вероятность того, что в урну были добавлены две исправных лампы, если все вынутые лампы оказались исправными.
Решение
А = {вытянутые лампы исправны};
Н1 = { при добавлении была добавлена 1 исправная лампа и 1 неисправная лампа } ![]() ;
;
Н2 = { при добавлении было добавлено 2 исправные лампы} ![]() ;
;
Н3 = { при добавлении было добавлено 2 неисправные лампы } ![]() ;
;
![]()
![]()
![]()
Пусть А – событие, состоит в том, что взятые лампы исправлены. Это событие наступит одновременно с наступлением одного из трех гипотез. Условные вероятности равны:
![]()
![]()
![]()
По формуле полной вероятности:
![]()
![]()
Б) Найти вероятность того, что в урну были добавлены две исправных лампы, если все вынутые лампы оказались исправными. Необходимо переоценить вероятности гипотез с учетом того, что добавлено 2 исправных лампы т. е. используем формулу Байеса:
![]()
Ответ: ![]() ;
; ![]()
3. В каждом из девяти независимых испытаний событие А происходит с постоянной вероятностью р = 0,32. Найти вероятность того, что событие А произойдет:
А) ровно четыре раза;
Б) более семи раз.
Решение
А) Вероятность того, что событие произойдет ровно 4 раза из 9, найдем по формуле Бернулли, т. к. число испытаний ![]() невелико
невелико ![]() , q =1 - 0.32=0.1, p=0.68:
, q =1 - 0.32=0.1, p=0.68:
![]()
Б) более семи раз
«более семи» раз означает или "ровно восемь" или "ровно девять" Поэтому:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: а) ![]() б)
б) ![]()
4. Дискретная случайная величина Х с математическим ожиданием М(х) = 4,95 задана законом распределения:
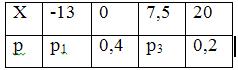
А) найти р1 и р3 и построить интегральную функцию распределения F(х);
Б) вычислить дисперсию D(x)
Решение
А) Запишем формулу математического ожидания:
![]()
![]()
Зная что, сумма всех вероятностей равна 1, запишем систему, где первое уравнение математическое ожидание, а второе сумма вероятностей:
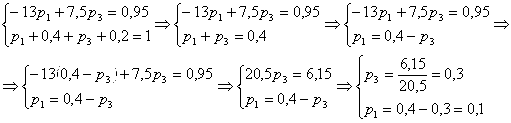
Выполним проверку:
![]()
Вероятности найдены правильно.
Интегральную функцию распределения
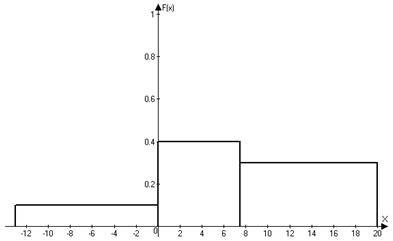
Б) Дисперсию найдем по формуле: ![]() .
.
![]()
Тогда ![]()
| < Предыдущая | Следующая > |
|---|