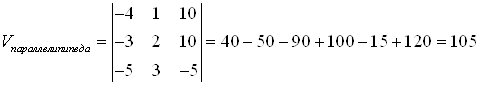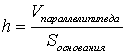Пределы, графики, дифференциальные уравнения, ряды, двойные интегралы, матрицы
Раздел I
Вычислить пределы числовых последовательностей.
6.16.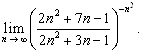 
Воспользуемся вторым замечательным пределом 
Вычислить пределы функций.
11.16 
Использовали 
при 
Вычислить пределы функций.
16.16. 
Решение
Сделаем замену 
При 
, 
Тогда 
Получим
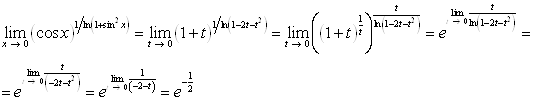
Использовали что 
при 
Раздел II
Найти производную.
11.16. 
Решение
Прологарифмируем левую и правую части 
Найдём производные от левой и правой части по х, считая у сложной функцией, зависящей от х:
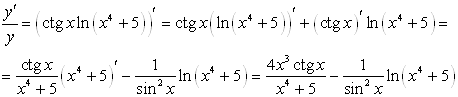
Отсюда: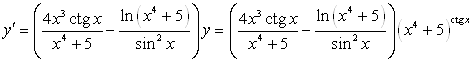 
Составить уравнения касательной и нормали к кривой в точке, соответствующей значению параметра 
.
16.16.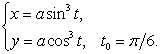 
Решение
Раздел III
Провести полное исследование функций и построить их графики.
8.16. 
Решение
- 1. Область определения:
2. 
- функция общего вида 3. Точки пересечения с осями: С осью ОХ 
, 
Промежутки знакопостоянства:
Найдём нули первой производной:
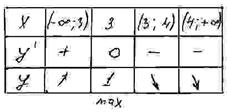
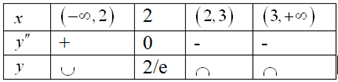
Точки 
- точка перегиба.
- 8. Строим график
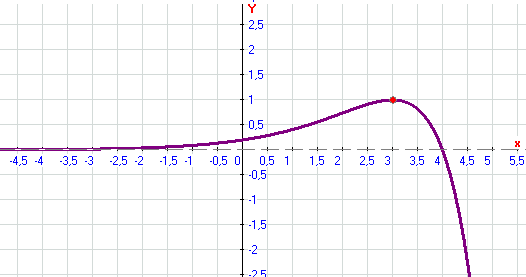
Раздел IV
Найти неопределенные интегралы
Решение
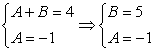
Вычислить определенные интегралы.
Решение
Вычислить определенные интегралы.
Решение
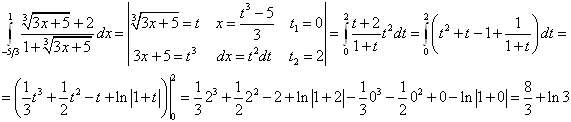
Раздел V
Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 
.)
Решение
- дифференциальное уравнение с разделяющимися переменными.
Разделим переменные и проинтегрируем:
Посчитаем отдельно:
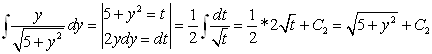
Тогда, общий интеграл : 
Найти решение задачи Коши.
Решение
- линейное дифференциальное уравнение.
Ищем решение в виде: 
, тогда 
. Подставим в исходное уравнение: 
. Отсюда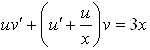 
.
Имеем 
Подставим начальніе условия: 
Получим окончательно, 
- решение задачи Коши.
Ответ:
Найти общее решение дифференциального уравнения.
Решение
Раздел VI
Найти область сходимости функционального ряда.
14.16. 
.
Решение
Общий член ряда 
. Используем радикальный признак Коши: 
или 
. То есть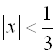 
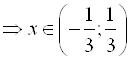- интервал сходимости ряда.
Исследуем сходимость ряда на концах интервала:
При 
ряд примет вид 
- расходится, так как не выполняется необходимое условие сходимости ряда 
.
При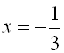 
ряд примет вид 
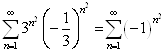- расходится, так как не выполняется необходимое условие сходимости ряда.
Ответ: область сходимости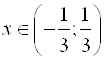 
Вычислить интеграл с точностью до 0,001.
20.16. 
.
Решение
Разложим интегральную функцию в ряд. Используем разложение в ряд Тейлора функции: 
Заменим разложение х на 
: 
Тогда:
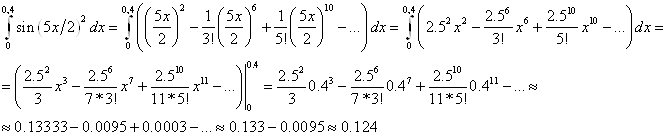
Так как 3й член ряда меньше 0,001
Ответ: 
Раздел VII
Найти объем тела, заданного ограничивающими его поверхностями.
11.16. 
Решение
Перейдём к циллиндрическим координатам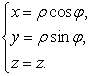 
Тогда 
, 
, 
По формуле 
. Имеем:
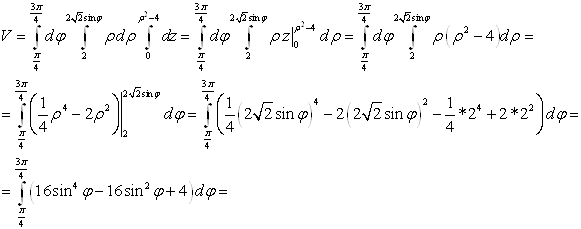
Найдём интегралы:
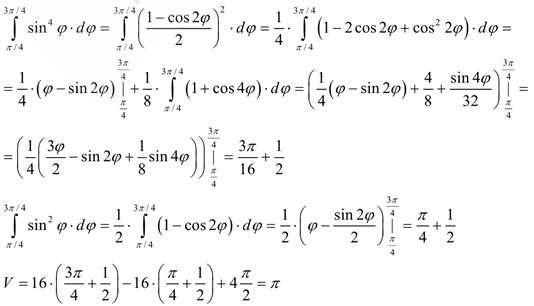
Ответ: 
(куб. ед.)
Тело V задано ограничивающими его поверхностями, m - плотность. Найти массу тела.
16.16. 
Решение
Изобразим данное тело
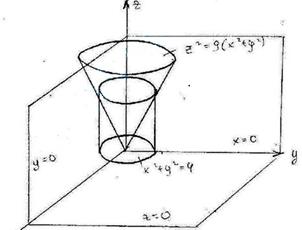
Проекция данного тела на плоскость хОу
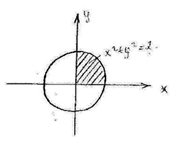
Перейдём к циллиндрическим координатам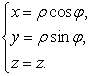
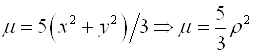
Как видно из рисунка 
, 
По формуле 
Тогда, искомая масса тела
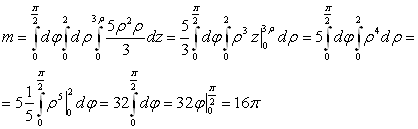
Раздел VIII
Найти угол между градиентами скалярных полей 
И 
В точке 
.
Решение
Найдём частные производные:
.В точке М: 
, тогда производные в данной точке:
.Найдём градиенты скалярних полей:
Поэтому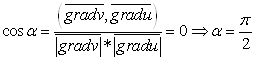 
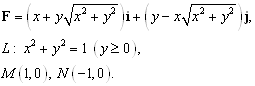
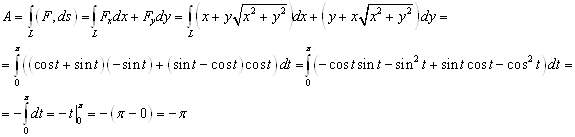
Найти работу силы 
при перемещении вдоль линии 
от точки 
к точке 
.
Решение
.
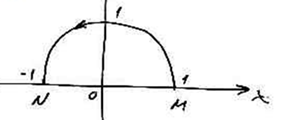
Работа
Ответ: 
Раздел IX
Вычислить площадь параллелограмма, построенного на векторах 
и 
.
Решение
Так как 
Ответ: 
(кв. ед.)
Вычислить объем тетраэдра с вершинами в точках 
и его высоту, опущенную из вершины 
на грань 
.
Найдём объём тетраэдра:
,
, 
Тогда 
Раздел X
Найти общее решение системы
3.16.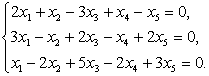 
Решение
Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:
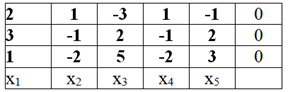
Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (-3). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой:
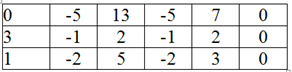
Умножим 2-ую строку на (-1). Умножим 3-ую строку на (3). Добавим 3-ую строку к 2-ой:
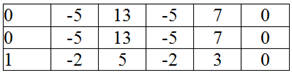
Умножим 1-ую строку на (-1). Добавим 2-ую строку к 1-ой:
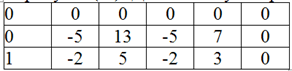
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 2. Поскольку ранг основной матрицы равен рангу расширенной, то Система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2, значит, неизвестные x1,x2 – зависимые (базисные), а x3,x4,x5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
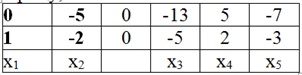
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
- 5x2 = - 13 x3 + 5 x4 - 7 x5
X1 - 2x2 = - 5 x3 + 2 x4 - 3 x5
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x1,x2 через свободные x3,x4,x5, то есть нашли Общее решение:
X2 = 13/5 x3- 1 x4 + 7/5 x5
X1 = 1/5 x3- 1/5 x5
Найти собственные значения и собственные векторы матрицы.
9.16.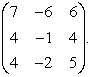 
Решение
Исходная матрица имеет вид: 
Составляем систему для определения координат собственных векторов:
(7 - λ)x1-6x2 + 6x3 = 0
4x1 + (-1 - λ)x2 + 4x3 = 0
4x1-2x2 + (5 - λ)x3 = 0
Составляем характеристическое уравнение и решаем его.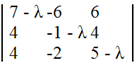 
Для этого находим определитель матрицы и приравниваем полученное выражение к нулю.
(7 - λ) • ((-1 - λ) • (5 - λ)-(-2 • 4))-4 • (-6 • (5 - λ)-(-2 • 6))+4 • (-6 • 4-(-1 - λ) • 6)=0
После преобразований, получаем:
-λ3+11•λ2-31•λ+21 = 0
λ1 = 1
Подставляя λ1 = 1 в систему, имеем: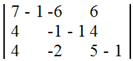 
Или 
Решаем эту систему линейных однородных уравнений
Выпишем основную матрицу системы:
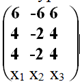
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (-2). Умножим 2-ую строку на (3). Добавим 2-ую строку к 1-ой: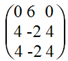 
Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой: 
Для удобства вычислений поменяем строки местами: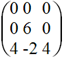 
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы. 
Найдем ранг матрицы.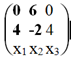 
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2, значит, неизвестные x1,x2 – зависимые (базисные), а x3 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор. 
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
6x2 = 0
4x1 - 2x2 = - 4
Методом исключения неизвестных находим Нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2 через свободные x3, то есть нашли Общее решение:
X2 = 0
X1 = - 1
Множество собственных векторов, отвечающих собственному числу λ1 = 1, имеет вид:
Где x3 - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x3 = 1:
λ2 = 3
Подставляя λ2 = 3 в систему, имеем:
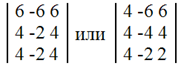
Решаем эту систему линейных однородных уравнений
Выпишем основную матрицу системы:
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (-1). Добавим 2-ую строку к 1-ой: 
Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой: 
Умножим 1-ую строку на (-1). Добавим 2-ую строку к 1-ой: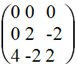 
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы. 
Найдем ранг матрицы.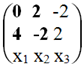 
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2, значит, неизвестные x1,x2 – зависимые (базисные), а x3 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.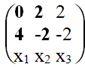 
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
2x2 = 2
4x1 - 2x2 = - 2
Методом исключения неизвестных находим Нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2 через свободные x3, то есть нашли Общее решение:
X2 = 1
X1 = 0
Множество собственных векторов, отвечающих собственному числу λ2 = 3, имеет вид:
Где x3 - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x3 = 1:
λ3 = 7
Подставляя λ3 = 7 в систему, имеем:
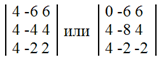
Решаем эту систему линейных однородных уравнений
Выпишем основную матрицу системы: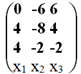 
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой: 
Добавим 2-ую строку к 1-ой: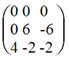 
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы. 
Найдем ранг матрицы.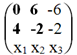 
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2, значит, неизвестные x1,x2 – зависимые (базисные), а x3 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.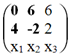 
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
6x2 = 6
4x1 - 2x2 = 2
Методом исключения неизвестных находим Нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2 через свободные x3, то есть нашли Общее решение:
X2 = 1
X1 = 1
Множество собственных векторов, отвечающих собственному числу λ3 = 7, имеет вид:
Где x3 - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x3 = 1:
| < Предыдущая | Следующая > |
|---|
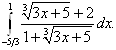
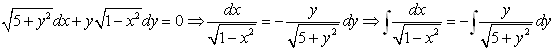
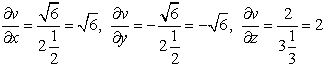
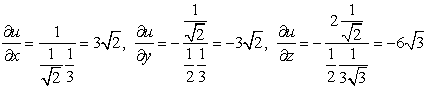