Первообразные и теория вероятности
1. Найти первообразные
А)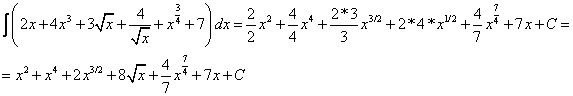 
Б)
В) 
Г) 
Разложим дробь 
на простые дроби
Тогда 
, получим
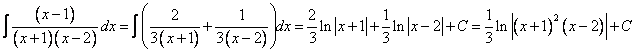
2. Вычислить определённые интегралы
А)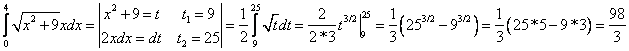 
Б)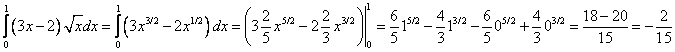 
3. Бросают игральную кость. Событие А – выпало нечётное число, В – выпало число меньшее 5. Найти 
,
,
,
, 
,
.
Имеем А={1; 3; 5}, B={1; 2; 3; 4}
Тогда 
, 
4. Случайным образом выбирают три шара из 12, среди которых 5 – белые и 7 – чёрные. Найти вероятность того, что среди выбранных два белых шара.
Общее число элементарных исходов испытания равно числу сочетаний из 12 элементов по 2, то есть 
.
Число исходов, благоприятствующих появлению двух белых шаров равно числу сочетаний из 5 элементов по 2, то есть 
.
Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов:
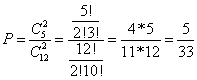
Ответ: 
5. Бросают две игральные кости. Найти вероятность событий А – сумма выпавших очков равна 4, В – произведение выпавших очков равно 4.
Решение
Всего имеется 36 равновероятных исходов.
Из них 3 исхода (1-3, 3-1, 2-2) с суммой 4.
И 3 исхода (1-4, 4-1, 2-2) с произведением выпавших очков 4.
По классической формуле определения вероятности
Вероятность 
. Вероятность 
Ответ: 
6. Два независимых события А и В наступают с вероятностями 0,4 и 0,8 соответственно. Найти вероятность того, что наступит а) хотя бы одно событие, б) ровно одно событие.
Решение
Б) Вероятность наступления ровно одного события найдём по формуле
. В нашем случае 
, 
. Тогда 
А) Вероятность наступления хотя бы одного события
Найдём вероятность не наступления ни события А ни В: 
.
Тогда вероятность противоположного события - вероятность наступления хотя бы одного события: 
Ответ: б) 
, а) 
7. Дан ряд распределения случайной величины 
:
|
|
-1 |
0 |
2 |
3 |
|
Р |
1/3 |
1/4 |
Р3 |
1/6 |
Найти Р3, функцию распределения 
, 
, 
, 
.
Решение
Так как сумма вероятностей Р1+Р2+Р3+Р4=1, то
Р3 =1-Р1+Р2+Р4=1-1/3-1/4-1/6=1/4
Тогда закон можно переписать в виде
|
|
-1 |
0 |
2 |
3 |
|
Р |
1/3 |
1/4 |
1/4 |
1/6 |
Функция распределения
Если 
, то 
;
Если 
, то 
;
Если 
, то 
.
Если 
, то 
;
Если 
, то
.
Вероятность 
Математическое ожидание дискретной случайной величины 
,
Имеем 
Дисперсия 
8. Дана плотность распределения:
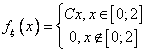
Найти С, , 
, , .
Решение
Для определения коэффициента С воспользуемся условием нормировки плотности распределения: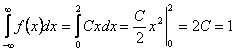 
, откуда 
.
Тогда, плотность распределения
Вероятность попадания величины на участок от 1 до 3 находим по формуле: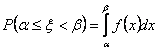 
;
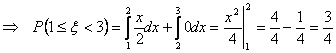Математическое ожидание непрерывной случайной величины 
Имеем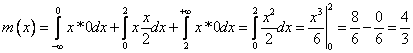 
Дисперсия непрерывной случайной величины 
Имеем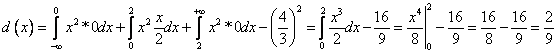 
9. Дан ряд распределения двумерной случайной величины 
|
|
1 |
2 |
3 | |
|
| ||||
|
-1 |
¼ |
0 |
¼ | |
|
0 |
1/8 |
P22 |
0 | |
|
1 |
1/8 |
1/8 |
0 |
Найти P22, частные распределения случайных величин , 
, , , 
, 
, а также корреляционный момент 
и коэффициент корреляции 
.
Решение
Так как сумма всех вероятностей должна равнятся 1, то
P22=1- P11 – P12 – P13 – P21 – P23 – P31 – P32 – P33=1-1/4-0-1/4-1/8-0-1/8-1/8-0=1/8.
Тогда ряд распределения двумерной случайной величины
|
|
1 |
2 |
3 | |
|
| ||||
|
-1 |
1/4 |
0 |
1/4 | |
|
0 |
1/8 |
1/8 |
0 | |
|
1 |
1/8 |
1/8 |
0 |
Сложив вероятности по столбцам, получим вероятности возможніх значений для , а сложив по строкам, получим вероятности возможніх значений для ,
|
|
1 |
2 |
3 |
|
Р |
1/2 |
1/4 |
1/4 |
|
|
-1 |
0 |
1 |
|
-1 |
1/2 |
1/4 |
1/4 |
| < Предыдущая | Следующая > |
|---|