Матрица линейного оператора. преобразование подобия. собственные значения и собственные векторы линейного оператора. диагонализация матриц
Задание 1. Линейный оператор ![]() преобразует векторы
преобразует векторы ![]() ,
, ![]() ,
, ![]() в векторы
в векторы ![]() ,
, ![]() ,
, ![]() . Найти матрицу
. Найти матрицу ![]() линейного оператора.
линейного оператора.
Решение. Матрицы
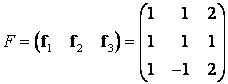 ,
, 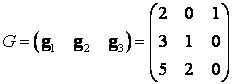 и
и ![]()
Связаны между собой соотношением ![]() , откуда
, откуда ![]() .
.
Так как ![]() , то
, то 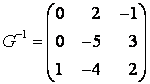 , а искомая матрица линейного оператора
, а искомая матрица линейного оператора 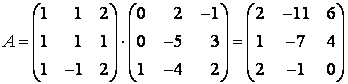 .
.
Ответ: .
Задание 2. Пусть линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей 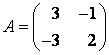 . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если матрица
, если матрица 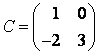 является матрицей перехода от базиса
является матрицей перехода от базиса ![]() к базису
к базису ![]() .
.
Решение. Матрицы ![]() и
и ![]() линейного оператора
линейного оператора ![]() , заданного в разных базисах, связаны между собой соотношением
, заданного в разных базисах, связаны между собой соотношением ![]() . Так как
. Так как 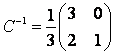 , то
, то
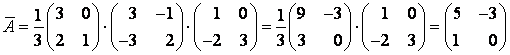 .
.
Ответ: 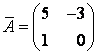 .
.
Задание 3. Линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей 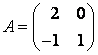 . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если
, если ![]() ,
, ![]() .
.
Решение. Связь между матрицами ![]() и
и ![]() линейного оператора в разных базисах определяется формулой
линейного оператора в разных базисах определяется формулой ![]() , где
, где ![]() – матрица перехода от базиса
– матрица перехода от базиса ![]() к базису
к базису ![]() .
.
Составим матрицу ![]() :
: 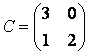 , тогда
, тогда 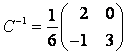 и, следовательно,
и, следовательно,
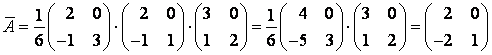 .
.
Ответ: 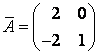 .
.
Задание 4. Линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей  . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если
, если ![]()
![]() ,
, ![]() .
.
Решение. Матрицы ![]() и
и ![]() связаны между собой соотношением
связаны между собой соотношением ![]() , где
, где ![]() – матрица перехода от базиса
– матрица перехода от базиса ![]() к базису
к базису ![]() .
.
Составим матрицу ![]() :
:  , тогда
, тогда  и, следовательно,
и, следовательно,


Ответ:  .
.
Задание 5. Найти собственные значения и собственные векторы линейного оператора ![]() , заданного в некотором базисе матрицей
, заданного в некотором базисе матрицей 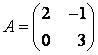 .
.
Решение. Для нахождения собственных значений линейного оператора составим характеристическое уравнение ![]() , т. е.
, т. е. 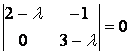 . Раскрывая определитель, получим
. Раскрывая определитель, получим ![]() , т. е.
, т. е. ![]() ,
, ![]() .
.
По определению ![]() называется собственным вектором линейного оператора
называется собственным вектором линейного оператора ![]() , соответствующим собственному значению
, соответствующим собственному значению ![]() , если
, если ![]() .
.
Найдём собственные векторы ![]() и
и ![]() , соответствующие собственным значениям
, соответствующие собственным значениям ![]() и
и ![]() .
.
При ![]() получим:
получим: 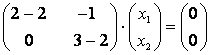 , что равносильно такой однородной системе уравнений:
, что равносильно такой однородной системе уравнений: 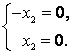
Если ![]() – базисная переменная, а
– базисная переменная, а ![]() – свободная, то
– свободная, то 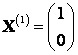 .
.
При ![]() :
: 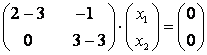 , что равносильно однородной системе уравнений
, что равносильно однородной системе уравнений 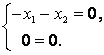
Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная. Примем
– свободная. Примем ![]() , тогда
, тогда ![]() , а следовательно,
, а следовательно,  .
.
Так как собственные векторы соответствуют различным собственным значениям, то они должны быть линейно независимы. Проверим линейную независимость полученных собственных векторов 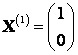 и
и  .
.
Составим матрицу  . Так как
. Так как ![]() , то собственные векторы
, то собственные векторы ![]() и
и ![]() линейно независимы.
линейно независимы.
Ответ: собственные числа ![]() ,
, ![]() ; собственные векторы
; собственные векторы 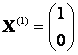 ,
,  .
.
Задание 6. Привести матрицу 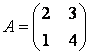 линейного оператора
линейного оператора ![]() к диагональному виду.
к диагональному виду.
Решение. Матрица линейного оператора будет диагональной в базисе из собственных векторов, если такой базис существует. Найдём собственные значения и собственные векторы линейного оператора.
Запишем характеристическое уравнение: 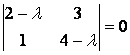 , т. е.
, т. е. ![]() или
или ![]() , откуда получаем
, откуда получаем ![]() ,
, ![]() .
.
Найдём собственные векторы ![]() И
И ![]() .
.
При ![]() получим:
получим:  , что соответствует следующей однородной системе уравнений:
, что соответствует следующей однородной системе уравнений: 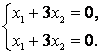
Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная. Полагая
– свободная. Полагая ![]() , получим
, получим 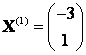 .
.
При ![]() :
: 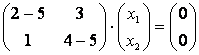 . Соответствующая однородная система уравнений имеет вид:
. Соответствующая однородная система уравнений имеет вид:
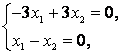
Откуда ![]() . Пусть
. Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная, примем
– свободная, примем ![]() тогда
тогда ![]() , а, следовательно,
, а, следовательно,  .
.
Собственные векторы ![]() и
и ![]() отвечают различным собственным значениям, поэтому они линейно независимы, т. е. могут составить базис. Матрица
отвечают различным собственным значениям, поэтому они линейно независимы, т. е. могут составить базис. Матрица ![]() линейного оператора в базисе из собственных векторов
линейного оператора в базисе из собственных векторов ![]() и
и ![]() имеет диагональный вид:
имеет диагональный вид: 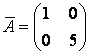 .
.
Можно проверить полученный результат. Так как ![]() , где матрица
, где матрица ![]() в случае перехода к базису из собственных векторов
в случае перехода к базису из собственных векторов 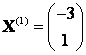 и
и  имеет вид
имеет вид  , следовательно,
, следовательно,
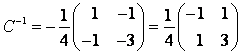 ,
,
Тогда
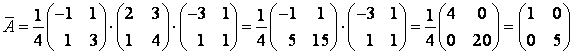 .
.
Ответ: 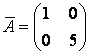 .
.
Задание 7. Найти собственные значения и собственные векторы линейного оператора ![]() , заданного в некотором базисе матрицей
, заданного в некотором базисе матрицей 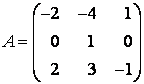 . Построить, если это возможно, базис из собственных векторов и найти матрицу
. Построить, если это возможно, базис из собственных векторов и найти матрицу ![]() этого линейного оператора в базисе из собственных векторов.
этого линейного оператора в базисе из собственных векторов.
Решение. Запишем характеристическое уравнение:
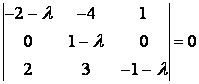 ,
,
Т. е. ![]() ,
, ![]()
![]() , откуда получаем
, откуда получаем ![]() ,
, ![]() ,
, ![]() .
.
Найдём собственные векторы линейного оператора.
При ![]() :
:  , тогда соответствующая однородная система уравнений примет вид:
, тогда соответствующая однородная система уравнений примет вид:
 или
или 
Что равносильно такой системе: 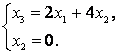
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Полагая
– свободная. Полагая ![]() , получим
, получим 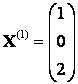 .
.
При ![]() :
: 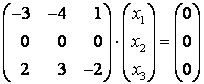 , или, переходя к однородной системе уравнений, получим
, или, переходя к однородной системе уравнений, получим
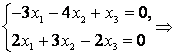
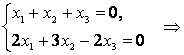
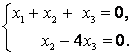
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Если
– свободная. Если ![]() , то
, то 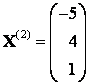 .
.
При ![]() получим:
получим: 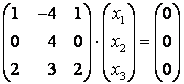 , и однородная система уравнений примет вид:
, и однородная система уравнений примет вид:


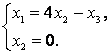
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Тогда если
– свободная. Тогда если ![]() , то
, то  . Найденные собственные векторы соответствуют различным собственным значениям, поэтому они линейно независимы, значит, существует базис из собственных векторов. Матрица перехода к такому базису
. Найденные собственные векторы соответствуют различным собственным значениям, поэтому они линейно независимы, значит, существует базис из собственных векторов. Матрица перехода к такому базису 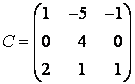 , тогда
, тогда
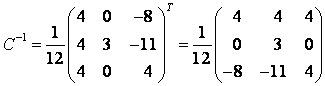 .
.
Матрица ![]() линейного оператора
линейного оператора ![]() в базисе из собственных векторов имеет вид:
в базисе из собственных векторов имеет вид:  .
.
Можно сделать проверку полученных результатов:
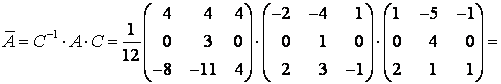

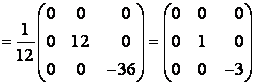 .
.
Ответ: ![]() ,
, ![]() ,
, ![]() ;
; 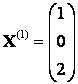 ,
, 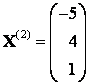 ,
,  ; матрица линейного оператора в базисе из собственных векторов
; матрица линейного оператора в базисе из собственных векторов  .
.
| < Предыдущая | Следующая > |
|---|