Квадратичные формы. приведение квадратичных форм к каноническому виду. критерий сильвестра
Задание 1. Составить матрицу квадратичной формы ![]() .
.
Решение. В общем виде квадратичная форма аргументов ![]() и
и ![]() задаётся следующим образом:
задаётся следующим образом:
![]() ,
,
Где ![]() являются элементами матрицы
являются элементами матрицы ![]() квадратичной формы. Сравнивая заданную квадратичную форму с общим её видом, получим, что
квадратичной формы. Сравнивая заданную квадратичную форму с общим её видом, получим, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , т. е.
, т. е.  .
.
Ответ:  .
.
Задание 2. Восстановить квадратичную форму по заданной матрице ![]() . Каждая ли из заданных матриц может соответствовать некоторой квадратичной форме? Почему?
. Каждая ли из заданных матриц может соответствовать некоторой квадратичной форме? Почему?
А)  ; б)
; б)  .
.
Решение. Матрица квадратичной формы должна быть симметрической, т. е. ![]() .
.
а) Матрица  не может быть матрицей квадратичной формы, так как
не может быть матрицей квадратичной формы, так как ![]() , т. е. она не является симметрической.
, т. е. она не является симметрической.
Б) Матрице  соответствует некоторая квадратичная форма, так как она является симметрической. Очевидно,
соответствует некоторая квадратичная форма, так как она является симметрической. Очевидно, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Следовательно, квадратичная форма примет вид
. Следовательно, квадратичная форма примет вид
![]() .
.
Ответ: ![]() .
.
Задание 3. Задана квадратичная форма ![]() . Найти квадратичную форму
. Найти квадратичную форму ![]() , полученную из данной линейным преобразованием:
, полученную из данной линейным преобразованием: ![]() ,
, ![]() .
.
Решение. При невырожденном линейном преобразовании ![]()
![]() матрица
матрица ![]() квадратичной формы преобразуется в матрицу
квадратичной формы преобразуется в матрицу ![]() .
.
Выпишем матрицу заданной квадратичной формы: 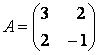 . Матрица заданного линейного преобразования
. Матрица заданного линейного преобразования  , тогда
, тогда 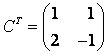 . Следовательно,
. Следовательно,
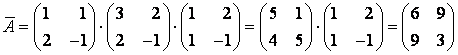 ,
,
т. е. ![]() .
.
Можно сделать проверку полученного результата непосредственной подстановкой в заданную квадратичную форму формулы преобразования координат:
![]() .
.
Ответ: ![]() .
.
Задание 4. Привести к каноническому виду квадратичную форму ![]() .
.
Решение. Выпишем матрицу ![]() квадратичной формы:
квадратичной формы: 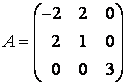 . Диагонализация матрицы
. Диагонализация матрицы ![]() квадратичной формы происходит в ОНБ из собственных векторов. Если
квадратичной формы происходит в ОНБ из собственных векторов. Если ![]() – матрица перехода к такому базису, то координаты вектора
– матрица перехода к такому базису, то координаты вектора ![]() в разных базисах связаны между собой соотношением:
в разных базисах связаны между собой соотношением:
 ,
,
Где в столбцах матрицы ![]() находятся координаты векторов ОНБ из собственных векторов, соответствующих собственным значениям.
находятся координаты векторов ОНБ из собственных векторов, соответствующих собственным значениям.
Составим характеристическое уравнение:
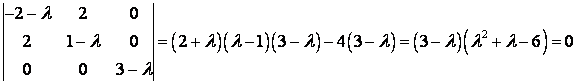 ,
,
Значит, собственные значения ![]() ,
, ![]() ,
, ![]() .
.
Найдём собственные векторы, соответствующие найденным собственным значениям.
При ![]() :
:  , откуда получаем однородную систему уравнений
, откуда получаем однородную систему уравнений 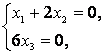 тогда
тогда 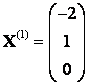 .
.
При ![]() :
:  , т. е.
, т. е. 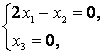 тогда
тогда 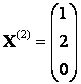 .
.
При ![]() :
: 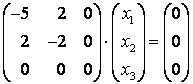 , откуда получаем однородную систему уравнений
, откуда получаем однородную систему уравнений


Из системы следует, что ![]() – свободная переменная. Примем
– свободная переменная. Примем ![]() , тогда
, тогда
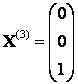 .
.
Векторы ![]() ,
, ![]() ,
, ![]() попарно ортогональны (в этом легко убедиться непосредственно!), тогда ОНБ составят векторы
попарно ортогональны (в этом легко убедиться непосредственно!), тогда ОНБ составят векторы
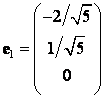 ,
, 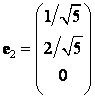 ,
, 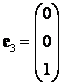 .
.
Матрица ![]() перехода от ОНБ
перехода от ОНБ ![]() к ОНБ
к ОНБ ![]() примет вид:
примет вид:
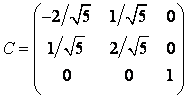 .
.
Замечание. О том чтобы матрица ![]() оказалась симметрической, следует помнить при построении собственных векторов
оказалась симметрической, следует помнить при построении собственных векторов ![]() ,
, ![]() И
И ![]() .
.
Формулы перехода от координат ![]() к координатам
к координатам ![]() :
:
![]() ,
, ![]() ,
, ![]() .
.
Канонический вид заданной квадратичной формы:
![]() .
.
Подстановкой приведенных формул преобразования координат в заданную квадратичную форму можно убедиться в правильности проведенных вычислений.
Ответ: ![]() .
.
Задание 5. Установить знакоопределённость квадратичной формы ![]() .
.
Решение.
Метод 1. Если все собственные значения ![]() , то квадратичная форма
, то квадратичная форма ![]() положительно определённая; если все
положительно определённая; если все ![]() – отрицательно определённая. Найдём собственные значения квадратичной формы. Для этого составим её матрицу:
– отрицательно определённая. Найдём собственные значения квадратичной формы. Для этого составим её матрицу:
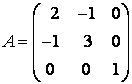
И характеристическое уравнение:
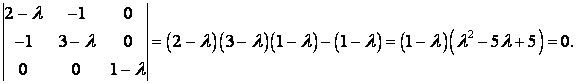
Его корни ![]() ,
, ![]() , т. е. все
, т. е. все ![]() , а следовательно, квадратичная форма положительно определённая.
, а следовательно, квадратичная форма положительно определённая.
Метод 2. Знакоопределённость квадратичной формы можно установить и с помощью критерия Сильвестра, в соответствии с которым квадратичная форма положительно определённая, если все главные диагональные миноры матрицы ![]() положительны, т. е.
положительны, т. е. ![]() ,
, 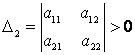 , …,
, …,  , а если знаки этих миноров чередуются, т. е.
, а если знаки этих миноров чередуются, т. е. ![]() ,
, ![]() ,
, ![]() , …, то квадратичная форма – отрицательно определённая.
, …, то квадратичная форма – отрицательно определённая.
Для данной квадратичной формы имеем:
![]() ,
, 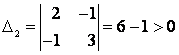 ,
, 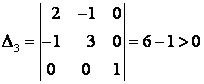 , т. е. заданная квадратичная форма положительно определённая.
, т. е. заданная квадратичная форма положительно определённая.
Ответ: квадратичная форма положительно определённая.
| < Предыдущая | Следующая > |
|---|