Контрольная работа по мат. анализу 10
1. Найти частные производные первого порядка следующих функций:
А) ![]() ;
;
Б) ![]() ; в)
; в) ![]() .
.
A)
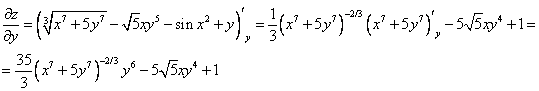
Б) ![]()
![]()
В) 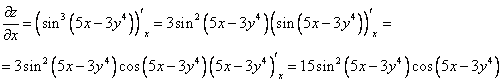
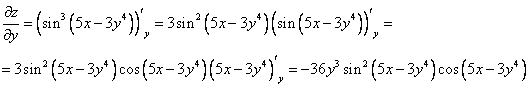
2. Найти дифференциалы первого и второго порядка от функции ![]() .
.
Воспользуемся следующими соотношениями для дважды дифференцируемых функций: ![]()
![]()
Таким образом,
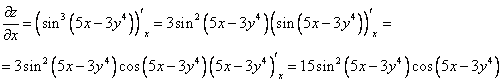
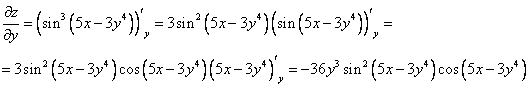



Тогда получим
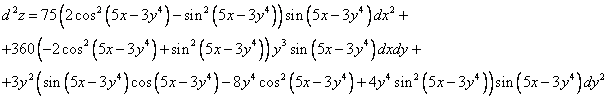
3. Вычислить определенные интегралы:
А) 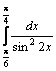 ; б)
; б)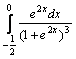 ; в)
; в)![]() ; г)
; г)![]() .
.
Решение
А) 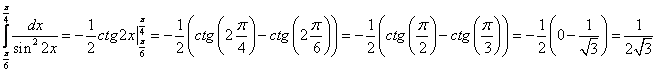 Б)
Б)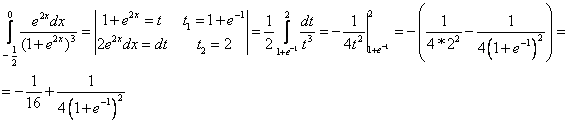 ;
;
В)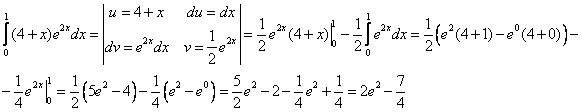 ;
;
Г) .
.
4. Вычислить или установить расходимость несобственных интегралов:
А) ![]() ; б)
; б) ![]() .
.
Решение
а) Данный интеграл – несобственный интеграл первого рода
 ;
;
Расходится
б) Данный интеграл – несобственный интеграл второго рода
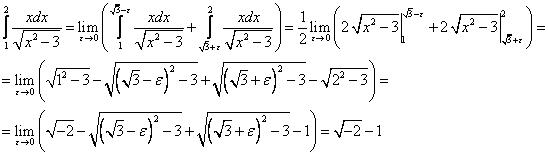 .
.
5. Найти площадь области, ограниченной кривыми:
А) ![]() ; б)
; б) ![]() .
.
Решение
А) Построим линии, ограничивающие фигуру.
![]() – парабола, симметричная относительно оси оу, вершина (0;0).
– парабола, симметричная относительно оси оу, вершина (0;0).
![]() – парабола, симметричная относительно оси оу, вершина (0;0).
– парабола, симметричная относительно оси оу, вершина (0;0).
![]() – прямая, проходящая через точку (0;2), параллельная оси очх.
– прямая, проходящая через точку (0;2), параллельная оси очх.
Изобразим фигуру, площадь которой нужно найти:
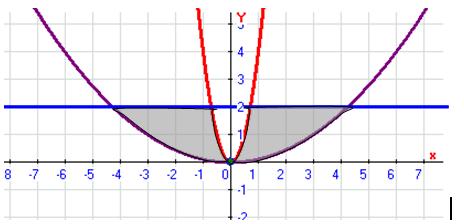
Данная область состоит из двух симметричных частей. Будем искать площадь фигуры при ![]()
По формуле ![]() . В нашем случае
. В нашем случае ![]() ,
, ![]() ,
, ![]() .
.
Получим 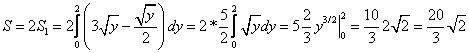 кв. ед.
кв. ед.
Б)Построим линии, ограничивающие фигуру
![]() - часть окружности
- часть окружности
![]() ,
, ![]() - часть кардиоиды
- часть кардиоиды
Изобразим фигуру, площадь которой нужно найти:
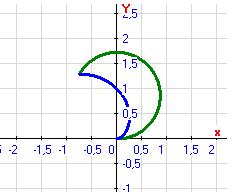
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то площадь области
, то площадь области ![]() вычисляется по формуле :
вычисляется по формуле : 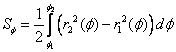 .
.
В нашем случае: ![]()
![]() ,
, ![]() ,
, ![]()
Получим: 
6. Найти длину дуги кривой ![]()
Решение
Изобразим данную дугу
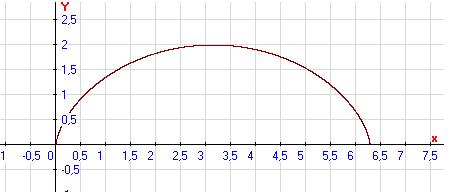
Если дуга кривой задана параметрическими уравнениями ![]() ,
, ![]() , в которых функции
, в которых функции ![]() Имеют непрерывные производные, то
Имеют непрерывные производные, то
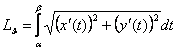 .
.
Найдём: ![]()
![]() ,
,
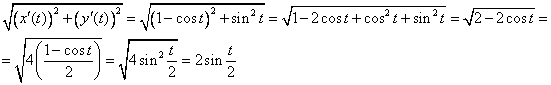
Тогда 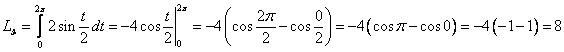
Ответ: ![]()
7. Определить объем тела, образованного вращением вокруг оси Оу Плоской фигуры, ограниченной линиями ![]() ,
, ![]() .
.
Решение
Построим ограничивающие линии.
![]() - парабола, вершина т. (0,1), ветви вниз
- парабола, вершина т. (0,1), ветви вниз
![]() - окружность, центр т. (0,0), радиус R=1;
- окружность, центр т. (0,0), радиус R=1;
Изобразим фигуру вращения:
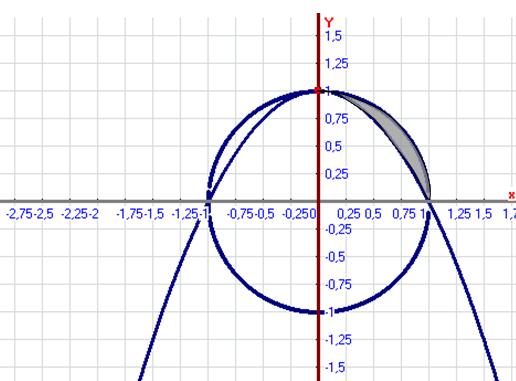
При вращении криволинейной трапеции (рис.11) вокруг оси OY образуется тело вращения.
Т. к. по условию криволинейная трапеция вращается вокруг оси OY, то объём тела вращения вычислим по формуле ![]() .
.
По условию ![]() ,
, ![]() . При этом
. При этом ![]() , т. е.
, т. е. ![]()
Тогда 
(ед3.)
| < Предыдущая | Следующая > |
|---|