Контрольная работа по мат. анализу (укр)

Тема 1. Диференційне числення функцій багатьох змінних.

Завдання 1. Знайти частинні похідні та функції .

Решение

Найдём и :

,

Завдання 2. Знайти частинні похідні , та функції .

Решение

Найдём , и :

, ,

Завдання 3. Знайти частинні похідні 2-го порядку , , , та перевірити, що : .

Решение

Найдём , , , :

, ,

, ,

, .

Тогда имеем , то есть

Завдання 4. Дослідити функцію на екстремум

Решение

Найдем Решив систему уравнений получим стационарную точку , то есть .

В этой точке выполнены необходимые условия экстремума. Найдем вторые частные производные

Вычислим . Так как , то точка является точкой локального минимума.

Тема 2. Подвійні, потрійні, криволінійні та поверхневі інтеграли.

Завдання 5. Обчислити подвійний інтеграл по області D, обмежений вказаними лініями:

А) , де .

Б) , де .

В) , де .

Решение

А) Изобразим данную область D:

Перейдём от двойного интеграла к повторному и вычислим его:

Ответ:

Б) Изобразим данную область D:

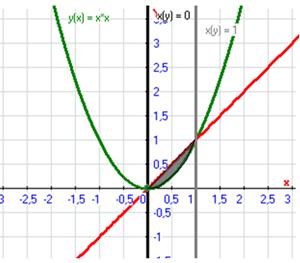
Перейдём от двойного интеграла к повторному и вычислим его:

Ответ:

В) , де .

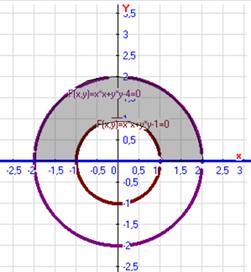
Перейдём от двойного интеграла к повторному, для этого перейдём к полярным координатам . Тогда

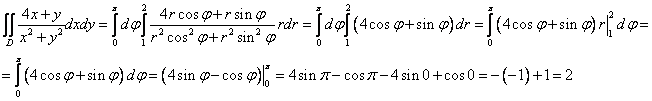Ответ:

Завдання 6. За допомогою потрійного інтегралу знайти об’єм області V, обмеженої поверхнями:

А) .

Б) .

Решение

А) Изобразим данное тело:

Проекция тела на плоскость :

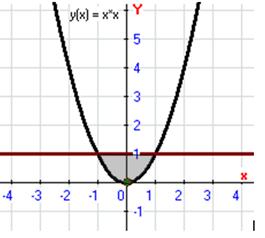
Тогда по формуле объем тела равен

Ответ: .

Б) Изобразим данное тело:

Тогда по формуле

Перейдём к циллиндрическим координатам:

Объем тела равен

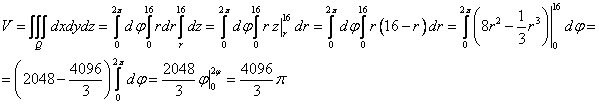
Ответ:

Завдння 7. Обчислити криволінійні інтеграли 1-го роду по вказаним лініям L:

А) , де

Б) , де .

Решение

А) По формуле

В нашем случае:

Ответ:

Б), .

По формуле

Ответ:

Завдння 8. Обчислити криволінійні інтеграли 2-го роду:

А) , де від точки до

Б) , де від точки до .

Решение

А) Y=X2 Þ Dy=2Xdx, XÎ[0;1].

Ответ:

Б) від точки до .

- параметрические уравнения кривой L (T изменяется от 0 до )

, . Тогда

Ответ:

Завдання 9. Знайти та :

Решение

Найдём . Тогда, по формулам,

Завдання 10. Знайти потік векторного поля через зовнішню сторону циліндричної поверхні та площинами . Застосувати теорему Остроградського–Гаусса.

Решение

Поток данного векторного поля через поверхность по теореме Гаусса-Остроградского равен: ,

, где .

Тогда

Перейдем к цилиндрической системе координат:

, ,

Ответ:

Завдання 11. Знайти градієнт скалярного поля .

Решение

По формуле , тогда

Завдання 12. Довести, що векторне поле є потенціальним та знайти його потенціал.

Решение

Поле является потенциальным, если выполнены следующие условия:

В нашем случае

Следовательно, поле потенциальное. Найдем его потенциал И, считая, что И(0;0;0) = 0:

Ответ:

Тема 3. Диференціальні рівняння.

Завдання 13. Знайти загальний розв’язок (загальний інтеграл) диференціального рівняння з відокремлювальними змінними.

Решение

Данное уравнение – дифференциальное уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем:

.

Тогда - искомый общий интеграл.

Ответ:

Завдання 14. Знайти загальний розв’язок лінійного диференціального рівняння 1-го порядку.

Решение

Данное уравнение – линейное дифференциальное уравнение.

Выполним замену , тогда . Подставим в исходное:

, .

Пусть функция такова, что сумма в скобках обращается в ноль. Решим уравнение .

Подставляя ее в уравнение , получим

,

Окончательно: .

Ответ:

Завдання 15. Знайти загальний інтеграл диференціального рівняння 1-го порядку

Решение

Данное уравнение – однородное дифференциальное уравнение.

Положим Y=Zx. Тогда Dy=Xdz+Zdx, сократив на и собрав члены при Dx и Dz получим:

Разделим переменные: .

Интегрируя, получим ;

Или

Заменив здесь Z на , получим общий интеграл заданного уравнения в виде .

Ответ:

Завдання 16. Знайти загальний розв’язок лінійного ДР 2-го порядку с постійними коефіцієнтами:

а), б), в).

Решение

А),

Характеристическое уравнение будет .

Его корни . Общее решение будет .

Б),

Характеристическое уравнение будет .

Его корни . Общее решение будет .

В).

Характеристическое уравнение будет .

Его корни . Общее решение будет .

Завдання 17. Розв’язати задачу Коші:

Решение

Соответствующее однородное

Характеристическое уравнение .

Общее решение однородного уравнения

Частное решение заданного уравнения ищем в виде , тогда , - подставим в исходное уравнение.

.

Тогда частное решение примет вид:

Общее решение исходного уравнения: .

Используем начальные условия: . Тогда

,

Для отыскания - решим систему уравнений:

Тогда, окончательно,

Ответ:

< Предыдущая		Следующая >