Интегральное исчисление 04
Билет № 28
1. Вычислить интеграл 
Применим универсальную тригонометрическую подстановку:
2. Вычислите первую производную функции 
Применим формулу дифференцирования сложной функции:
3. Вычислить предел по правилу Лопиталя 
Решение:
Пусть 
.
4. Провести нормаль к линии 
параллельно прямой 
.
Решение:
Определим угловой коэффициент заданной прямой:
.
Итак, угловой коэффициент нормали должен быть равен 1. Уравнение нормали к графику функции 
в точке 
имеет вид:
.
Итак,
.
Вычислим производную заданной функции:
.
Найдем точку, в которой будет проведена нормаль:
.
Запишем уравнение нормали:
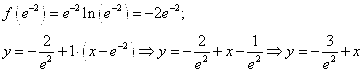
5. Найти промежутки возрастания и убывания функции 
Решение:
Область определения функции вся числовая прямая. Найдем первую производную:
Итак, первая производная всюду на всей числовой прямой. Тогда функция возрастает при всех 
.
6. Определить асимптоты кривой 
Решение:
Область определения: 
. Тогда 
– вертикальная асимптота.
Наклонные или вертикальные асимптоты:
Итак, наклонная асимптота 
7. Вычислить интеграл 
Решение:
Сделаем замену:
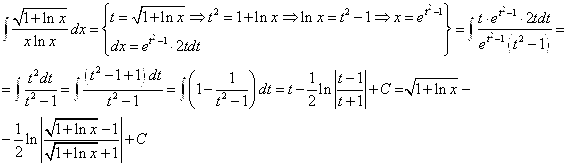
8. Вычислить приближенно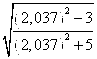 
.
Решение:
Введем функцию:
Применим первый дифференциал:
| < Предыдущая | Следующая > |
|---|
