|
1. Предприятие обратилось 1 марта в банк за кредитом в 150 тыс. руб., обязуясь вернуть сумму с процентами в конце года (31 декабря). Какой способ начисления простых процентов 365/365, 365/360 или 360/360 выгоден для предприятия и какой - для банка, если используется простая процентная ставка 26 % годовых и год не високосный?
|
Дано:
P = 150 тыс. руб.
Т1 = 01.03
Т2 = 31.12
I = 26 % = 0,26
S - ?
|
Решение:
Для нахождения наращенной суммы воспользуемся формулой наращения по простым процентам, или формулой простых процентов:
S = P(1+i ,где
S – наращенная сумма;
P – первоначальная сумма кредита;
I – процентная ставка;
T – период начисления в днях;
K – продолжительность года в днях.
1) английскую практику начисления процентов или точные проценты с точным числом дней ссуды, когда продолжительность года и продолжительность ссуды берутся точно по календарю. (365/365)
01.03 – 60 день в году
31.12 – 365 день
T = 365 - 60 = 305 дней
S = 150 000 (1+0,26 ) = 182 589,04 руб.
2) французская практика начисления процентов или Обыкновенные проценты с точным числом дней ссуды, когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю. (365/360)
T = 109 дней
S = 150 000 (1+0,26 ) = 183 041,67 руб.
3) германская практика начисления процентов или обыкновенные проценты с приближенным числом дней ссуды или, когда продолжительность года условно принимается за 360 дней, а целого месяца – за 30 дней. (360/360)
T = 30 – 1 +30*8+31= 300 дней
S = 150 000 (1+0,26 ) = 182 500 руб.
|
Ответ: для предприятия выгоден способ начисления простых процентов 360/360, т. к. ему необходимо будет вернуть 182500 руб. Для банка выгоден способ начисления простых процентов – 365 / 360, т. к. предприятие вернет банку 183 041,67 руб.
2. В банк предлагаются для учета два векселя: на сумму 30 тыс. руб. со сроком погашения через 60 дней и на сумму 34 тыс. руб. со сроком погашения через 240 дней. При каком способе дисконтирования: а) по учетной ставке, б) по процентной ставке банк при учете этих векселей выплатит одинаковые суммы, если расчетное число дней в году равно 360?
|
Дано:
S1 = 30 тыс. руб.
N1 = 60 дней
S2 = 34 тыс. руб.
N2 = 240 дней
К = 360
S - ?
|
Решение:
Т. к. выплаты одинаковы, составим следующие равенства:
А) Выплаты по учтенной ставке определяются по следующей формуле:
P = S (1 - d,
Где S – номинал векселя;
Р – сумма, полученная векселедержателем;
D – простая учетная ставка;
t –срок погашения в днях;
K – продолжительность года в днях.
30 (1 - d = 34 (1 - d
30 - 5d = 34 – 22,67d
- 5d + 22,67d = 34 – 30
17,67d = 4/17,67
D = 0,2264 или 22,64%
Б) Выплаты по процентной ставке определяются по следующей формуле:
Р =  ,
Где i – простая процентная ставка.
 = >
30(1+0,667i) = 34(1+0,167i)
30 + 20,01i = 34+5,678i
20,01i – 5,678i = 34 – 30
14,332i = 4 / 14,332
I = 0,2791 или 27,91%
|
Ответ: при учете векселей выплатит одинаковые суммы а) при простой учетной ставке равной 22,64%, б) при простой процентной ставке – 27,91%
3. Банк предоставил ссуду в размере 150 тыс. руб. на 39 месяцев под процентную ставку 30% годовых на условиях единовременного возврата основной суммы долга и начисленных сложных процентов. Какую сумму предстоит вернуть банку при различных вариантах начисления сложных процентов: а) годовом; б) полугодовом; в) ежеквартальном.
|
Дано:
Р = 150 тыс. руб.
N = 39 месяцев
I = 30% = 0,3
A) m = 1
Б) m = 2
В) m = 4
S - ?
|
Решение:
Наращенная сумма определяется по следующей формуле:
S = P ,
Где S – наращенная сумма;
Р – первоначальная сумма;
J – номинальная ставка процентов;
N – срок ссуды;
M – интервал начисления процентов.
39 месяцев – это 3,25 года
А) S = 150000 351890,19 руб.
Б) S = 150 000 372 072,20 руб.
В) S = 150000 384 061,96 руб.
|
Ответ: наращенная сумма равна а) 351890,19 руб.; б) 372072,20 руб.; в) 384061,96 руб.
4. Имеется обязательство выплатить суммы 60 тыс. руб. и 90 тыс. руб. соответственно через 3 года и 5 лет. По обоюдному согласию стороны пересматривают порядок выплат: 15 тыс. руб. выплачиваются через 1 год 6 месяцев, 45 тыс. руб. - через 2 года, 50 тыс. руб. - через 6 лет, остаток долга погашается через 7 лет. Определите величину четвертого платежа, если на деньги начисляются ежеквартально сложные проценты по годовой номинальной процентной ставке 32 %
|
Дано:
Sj1 = 60 тыс. руб.
Nj1 = 3 года
Sj2 = 90 тыс. руб.
Nj2 = 5 лет
Sk1= 15 тыс. руб.
Nk1 = 1,5 года
Sk2= 45 тыс. руб.
Nk2 = 2 года
Sk3= 50 тыс. руб.
Nk3 = 6 лет.
Nk4 = 7 лет
J = 32% = 0,32
M = 4
Sk4 - ?
|
Решение:
Уравнение эквивалентности платежей общего в вида при использовании сложной процентной ставке имеет вид:
 ,
Где Sj и nj – параметры заменяемых платежей;
Sk и nk – параметры заменяющих платежей.
Составим равенство:
 =  +
23,81+19,31 = 9,4+24,32+7,89 + 0,12S
0,12S = 43,12 – 41,61
0,12S = 1,51 / 0,12
S = 12,58 тыс. руб.
|
.Ответ: величина четвертого платежа равна 12,58 тыс. руб.
5. Банк предлагает ренту постнумерандо на 10 лет с квартальной выплатой 4 тыс. руб. Годовая процентная ставка в течение всего периода остается постоянной, и сложные проценты начисляются ежеквартально. По какой цене можно приобрести эту ренту сейчас, если выплаты начнут осуществляться немедленно, а сложная процентная ставка равна 32 % годовых?
|
Дано:
R = 4 тыс. руб.
N = 10 лет
P=m = 4
J = 32% = 0,32
S - ?
|
Решение:
Так как количество выплат в год равно интервалу начисления процентов (p=m), современную стоимость ренты определим по следующей формуле:
Где А –современная стоимость ренты;
R – размер платежа; ты
J – номинальная ставка процентов;
N – срок ре;
M – интервал начисления процентов.
 47700 руб.
|
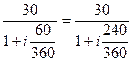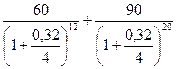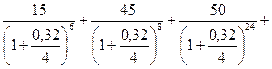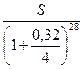
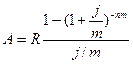
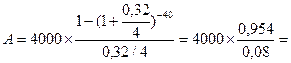Ответ: цена ренты равна 47700 руб.
|
