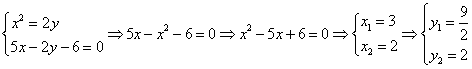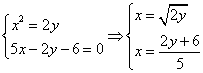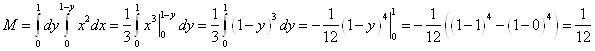Двойные интегралы, векторные поля 02

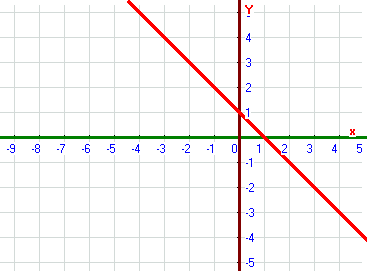
Изобразим данную область

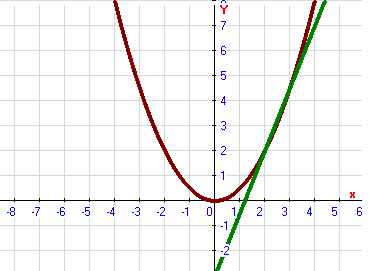
Найдём точки пересечения данных линий:

Расставим пределы интегрирования:

Внутренний интеграл по dx, внешний по dy:

Из уравнения

Тогда , получим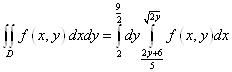

Внутренний интеграл по dy, внешний по dx:

Из уравнения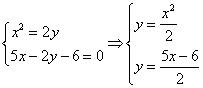

Тогда , получим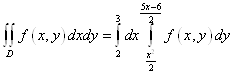

Изобразим данную пластинку:

По формуле

Тогда, , , получим

Ответ:

Решение

Изобразим данную пластину

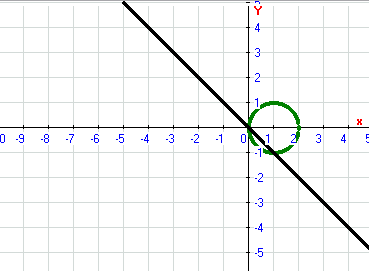
Перейдем к полярным координатам

Уравнение окружности в полярных координатах

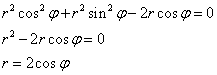
Уравнение прямой в полярных координатах

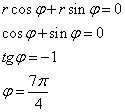
Находим статический момент

Ответ:

Решение

Изобразим данные поверхности:

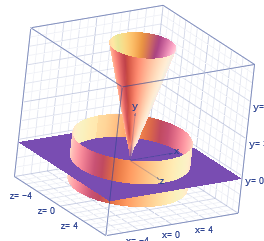
По формулам

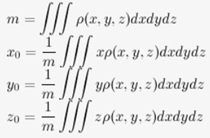
Перейдем к цилиндрическим координатам 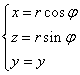, тогда ,

В нашем случае

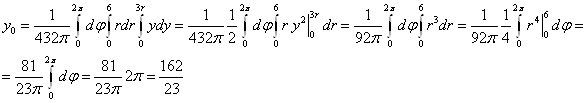
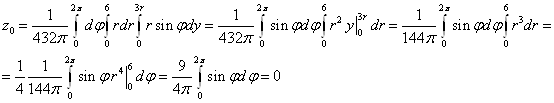
Ответ: Искомая точка координат центра масс:

Решение

Изобразим данное тело:

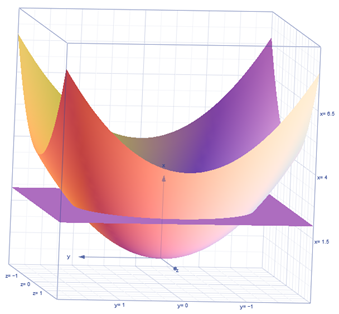
Момент инерции относительно оси ОX найдём по формуле

Перейдем к цилиндрическим координатам 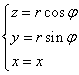, тогда ,

В нашем случае

Решение

Изобразим данное тело:

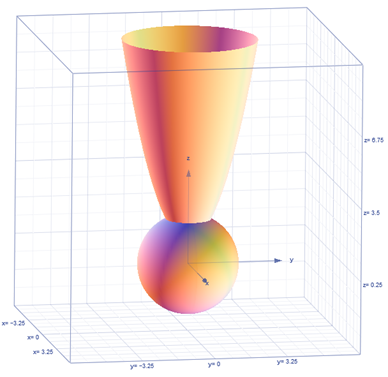
Линия пересечения данных поверхностей:

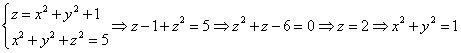
Тогда, по формуле Получим

Тело симметрично относительно плоскости YОZ и XOZ. Поэтому

Поскольку область интегрирования S четвёртая часть круга, то целесобразно перейти к полярным координатам . Тогда ,

куб. ед.

Ответ: куб. ед.

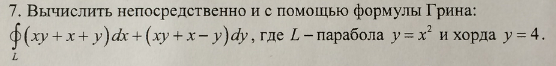
Решение

Изобразим данный контур

По формуле Грина

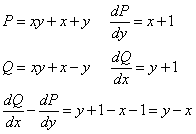
Тогда

Найдём теперь значение криволинейного интеграла непосредственно по контуру прямоугольника

На АВ: , ,

На BC: , , x от 2 до -2

На CA: , , х от -2 до 0

Тогда

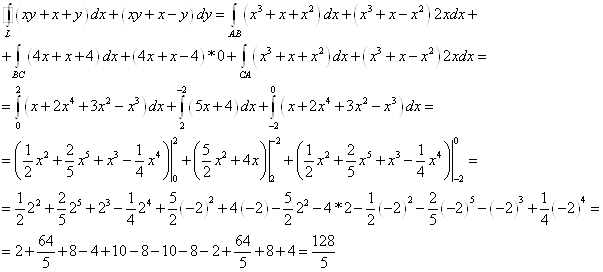
Ответ:

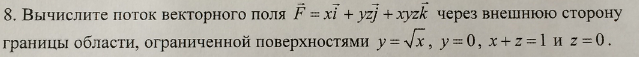
Решение

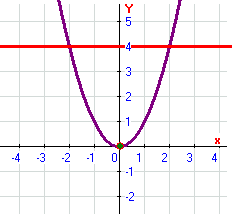
Изобразим данные поверхности:

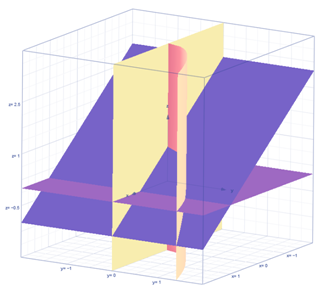
Проекция на плоскость ХОУ

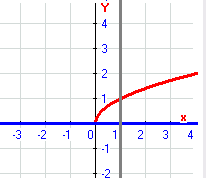
Применим формулу Остроградского-Гаусса

По формуле Остроградского имеем

Ответ:

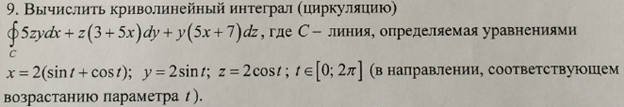
Решение

Решение

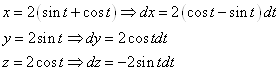. Тогда получим

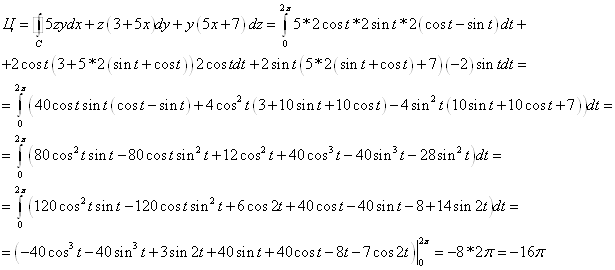
Ответ:

Решение

Дивергенция

Поле не соленоидальное

Ротор

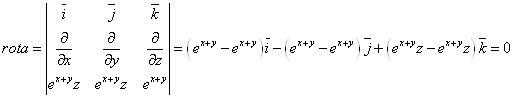
- поле безвихревое, а следовательно, и потенциальное.

Найдём потенциал данного поля

Поскольку поле потенциально, то его потенциал можно найти по формуле

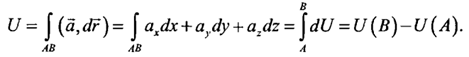
Где в качестве пути интегрирования возьмём ломаную ОАВМ, состоящую из отрезков прямых, параллельных координатным осям

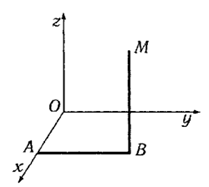
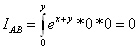
Таким образом,

< Предыдущая		Следующая >