Дифференциальные уравнения (4 примера)

8. Найти общее решение дифференциального уравнения первого порядка (уравнения с разделяющимися переменными, однородные и линейные)

Решение

Данное дифференциальное уравнение – однородное.

Приведём уравнение к виду:

Полагаем . Тогда . Подставляя в уравнение, получим:

- получили уравнение с разделяющимися переменными. Разделим переменные: . Интегрируем: Следовательно:

Возвращаясь к старой переменной , получим: .

Ответ:

38. Найти общее решение дифференциального уравнения первого порядка (уравнения с разделяющимися переменными, однородные и линейные)

Решение

Данное дифференциальное уравнение – однородное.

Приведём уравнение к виду: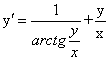

Полагаем . Тогда . Подставляя в уравнение, получим:

- получили уравнение с разделяющимися переменными. Разделим переменные: . Интегрируем: Следовательно:

Возвращаясь к старой переменной , получим: 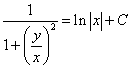или

Ответ:

68. Найти частное решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

, ,

Решение

Найдём решение соответствующего однородного уравнения. Его характеристическое уравнение имеет корни , . Тогда общее решение однородного уравнения имеет вид: .

Частное решение неоднородного уравнения будем искать в виде: , тогда ,

Подставим в исходное:

, .

Приравнивая коэффициенты при одинаковых степенях х получим систему:

,

,

Тогда , .

Частное решение имеет вид:

Общее решение будет иметь вид:

Так как по условию , то ,

Так как по условию , а то ,

Решим систему:

Получим:

Окончательно:

Ответ:

78. Найти частное решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

, ,

Решение

Найдём решение соответствующего однородного уравнения. Его характеристическое уравнение имеет корни , . Тогда общее решение однородного уравнения имеет вид: .

Уравнение имеет вид

Найдём частное решение для правой части

Частное решение неоднородного уравнения будем искать в виде: , тогда ,

Подставим в исходное:

,. Следовательно:

Частное решение имеет вид:

Найдём частное решение для правой части

Частное решение неоднородного уравнения будем искать в виде: , тогда ,

Подставим в исходное:

,.

Приравнивая коэффициенты при одинаковых степенях х получим систему:

,

,

Тогда , .

Частное решение имеет вид:

Общее решение будет иметь вид:

Так как по условию , то ,

Так как по условию , а то ,

Решим систему:

Получим:

Окончательно:

Ответ:

< Предыдущая		Следующая >