Дифференциальное исчисление 02

№4

1.  Найти частные производные функции

Решение

2.  Найти и , если, где

Решение

3.  Найти экстремумы функции

Решение

Найдем частные производные функции .

Решим систему уравнений.

2x+3y2-15 = 0

6xy-12 = 0

Получим:

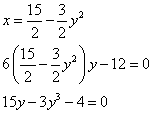
Полученное уравнение не имеет действительных корней, следовательно, функция не имеет экстремумов

4.  Найти производную функции в точке в направлении, составляющем одинаковые углы со всеми координатными осями.

Решение

По формуле, производная в т. М. по направлению вектора имеет вид

Найти направление вектора - значит найти его направляющие косинусы:

По условию - вектор, составляющий одинаковые углы со всеми координатными осями.

Модуль вектора |a| равен: , тогда направляющие косинусы:

Найдём ,

Окончательно,

5.  Написать уравнение касательной плоскости и нормали к поверхности

в точке

Решение

Запишем уравнения касательной в общем виде:

Z - z0 = f'x(x0,y0,z0)(x - x0) + f'y(x0,y0,z0)(y - y0)

По условию задачи x0 = π/4, y0 = π/4, тогда z0 = 1/2

Найдем частные производные функции z = f(x, y) = sin(x)*cos(y):

F'x(x, y) = (sin(x)•cos(y))'x = cos(x)•cos(y)

F'x(x, y) = (sin(x)•cos(y))'y = - sin(x)•sin(y)

В точке М0(π/4,π/4) значения частных производных:

F'x(π/4;π/4) = 1/2

F'y(π/4;π/4) = -1/2

Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:

Z - 1/2 = 1/2(x - π/4) + -1/2(y - π/4) или -1/2•x+1/2•y+z-1/2 = 0

Запишем уравнения нормали в общем виде:

Пользуясь формулой, получаем канонические уравнения нормали к поверхности в точке М0:

< Предыдущая		Следующая >