2.2 Базис и координаты на прямой, плоскости и в пространстве
Пусть на плоскости задан ненулевой вектор ![]() , тогда для любого вектора
, тогда для любого вектора ![]() , лежащего на этой же прямой, существует единственное вещественное число
, лежащего на этой же прямой, существует единственное вещественное число ![]() , такое, что
, такое, что
![]() , (1)
, (1)
При этом ![]() называют базисным вектором,
называют базисным вектором, ![]() – координатой
– координатой ![]() относительно базиса
относительно базиса ![]() .
.
Если на плоскости заданы два ненулевых, неколлинеарных вектора ![]() и
и ![]() , то для любого вектора
, то для любого вектора ![]() , лежащего в этой же плоскости, существует единственная пара чисел
, лежащего в этой же плоскости, существует единственная пара чисел ![]() и
и ![]() , таких, что
, таких, что
![]() , (2)
, (2)
При этом совокупность ![]() ,
, ![]() называется базисом,
называется базисом, ![]() – координатами
– координатами ![]() относительно этого базиса. Подчеркнем, что так как
относительно этого базиса. Подчеркнем, что так как ![]() и
и ![]() неколлинеарны, то они линейно независимы.
неколлинеарны, то они линейно независимы.
Если в пространстве заданы три ненулевых, некомпланарных (а, следовательно, линейно независимых) вектора ![]() , то для любого вектора
, то для любого вектора ![]() существует единственная тройка чисел
существует единственная тройка чисел ![]() таких, что
таких, что
![]() , (3)
, (3)
При этом совокупность ![]() называется базисом,
называется базисом, ![]() – координатами
– координатами ![]() относительно этого базиса.
относительно этого базиса.
Линейные комбинации вида (1), (2), (3) называют разложением вектора ![]() по базису.
по базису.
Объединяя три случая, можно дать следующее определение:
Определение. Коэффициенты линейной комбинации, при помощи которой вектор ![]() выражается через базис, называются координатами вектора
выражается через базис, называются координатами вектора ![]() относительно этого базиса.
относительно этого базиса.
Теорема 5. Линейные операции над векторами сводятся к таким же операциям над их соответствующими координатами.
Введенные базисы на плоскости и в пространстве называют аффинными. Аффинный базис называется декартовым, если он состоит из единичных взаимно перпендикулярных векторов. Векторы декартова базиса обозначают ![]() . Координаты вектора
. Координаты вектора ![]() относительно декартова базиса обозначают через
относительно декартова базиса обозначают через ![]() .
.
Определение. Система, состоящая из произвольной точки 0 и векторного аффинного базиса пространства, называется аффинной системой координат этого пространства, точка 0 – начало аффинной системы координат.
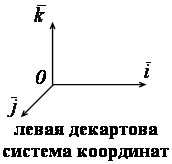 |

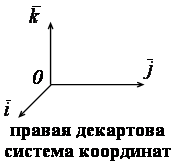 |
Аффинная система координат называется декартовой, если ее векторный базис – декартов.
Определение. Радиус-вектором точки ![]() в аффинной или декартовой системе координат называется вектор
в аффинной или декартовой системе координат называется вектор ![]() , где
, где ![]() – начало системы координат.
– начало системы координат.
Определение. Координатами точки ![]() относительно некоторого базиса называются координаты ее радиус-вектора относительно этого базиса.
относительно некоторого базиса называются координаты ее радиус-вектора относительно этого базиса.
Теорема 6. Координаты вектора равны разностям соответствующих координат его конца и начала.
Пример 9. Заданы векторы ![]() и
и ![]() . Убедиться, что они коллинеарны и найти разложение
. Убедиться, что они коллинеарны и найти разложение ![]() по базису
по базису ![]() .
.
Решение. У коллинеарных векторов координаты пропорциональны. В нашем случае 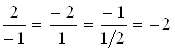 , следовательно,
, следовательно, ![]() .
.
Пример 10. Относительно некоторого базиса даны векторы ![]() ,
, ![]() и
и ![]() . Убедиться, что векторы
. Убедиться, что векторы ![]() и
и ![]() можно взять за базис и найти координаты
можно взять за базис и найти координаты ![]() в этом базисе.
в этом базисе.
Решение. Координаты ![]() и
и ![]() не пропорциональны, следовательно,
не пропорциональны, следовательно, ![]() не параллелен
не параллелен ![]() , значит, они линейно независимы и их можно принять за базис. Обозначим искомые координаты
, значит, они линейно независимы и их можно принять за базис. Обозначим искомые координаты ![]() через
через ![]() и
и ![]() , тогда
, тогда ![]() . По теореме 5 получим систему
. По теореме 5 получим систему 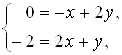 из которой находим
из которой находим ![]() ;
; ![]() .
.
Пример 11. В декартовом базисе ![]() заданы векторы
заданы векторы ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
1. Найти координаты вектора ![]() в базисе
в базисе ![]() .
.
2. Убедиться, что векторы ![]() образуют базис.
образуют базис.
3. Найти координаты вектора ![]() в базисе
в базисе ![]() и написать разложение
и написать разложение ![]() по этому базису.
по этому базису.
Решение. 1. Вектор ![]() является линейной комбинацией векторов
является линейной комбинацией векторов ![]() , следовательно,
, следовательно, ![]() или
или ![]() .
.
2. Базис состоит из линейно независимых векторов, значит линейная комбинация векторов ![]() обратится в
обратится в ![]() только если все коэффициенты этой линейной комбинации равны нулю. Найдем эти коэффициенты из условия
только если все коэффициенты этой линейной комбинации равны нулю. Найдем эти коэффициенты из условия ![]() ,
, ![]()
![]() Или
Или ![]() . Так как
. Так как ![]() – линейно независимы, то это равенство возможно, если все коэффициенты обратятся в
– линейно независимы, то это равенство возможно, если все коэффициенты обратятся в ![]() :
: ![]() , следовательно,
, следовательно, ![]() – линейно независимы и образуют базис.
– линейно независимы и образуют базис.
3. Разложение вектора ![]() по базису
по базису ![]() имеет вид:
имеет вид: ![]() , где
, где ![]() – координаты вектора
– координаты вектора ![]() в этом базисе. По теореме 5 имеем:
в этом базисе. По теореме 5 имеем: 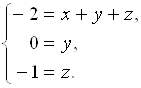
Решая эту систему, найдем ![]() , т. е.
, т. е. ![]() ,
, ![]() .
.
Пример 12. Вектор ![]() отложен от точки
отложен от точки ![]() . Конец его оказался в точке
. Конец его оказался в точке ![]() . Найти координаты точки
. Найти координаты точки ![]() .
.
Решение. Обозначим координаты точки ![]() через
через ![]() . По теореме 6:
. По теореме 6: ![]() ,
, ![]() ,
, ![]() , откуда
, откуда ![]() .
.
Пример 13. Даны точки ![]() ,
, ![]() . Найти значения
. Найти значения ![]() и
и ![]() , при которых точка
, при которых точка ![]() , лежит на прямой
, лежит на прямой ![]() .
.
Решение. Векторы ![]() и
и ![]() коллинеарны, следовательно
коллинеарны, следовательно 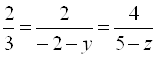 , откуда
, откуда ![]() ,
, ![]() .
.
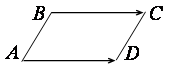 Пример 14. Даны три последовательные вершины параллелограмма
Пример 14. Даны три последовательные вершины параллелограмма ![]() ,
, ![]() ,
, ![]() . Найти координаты четвертой вершины
. Найти координаты четвертой вершины ![]() .
.
Решение. Пусть ![]() , тогда
, тогда ![]() ,
, ![]() . Так как
. Так как ![]() , то их соответствующие координаты равны, поэтому
, то их соответствующие координаты равны, поэтому ![]() ,
, ![]() ,
, ![]() . Откуда
. Откуда ![]() .
.
| < Предыдущая | Следующая > |
|---|