2.1. Методы решения нелинейных уравнений. Метод деления пополам (метод бисекций)

Задача. Найти решение нелинейного уравнения с точностью .

Метод состоит в следующем: в результате отделения корня найден отрезок [a, b], в котором расположено искомое значение корня. В качестве начального приближения корня возьмем значение co=(b+a)/2. Далее исследуем значения на концах отрезков [a, co] и [co, b]. Тот из них, на концах которого примет значения разных знаков, содержит искомый корень. Поэтому его принимают в качестве нового отрезка (см. рис. 1, здесь корень находится на отрезке [co, b]). Затем полученный отрезок делим пополам и вновь производим проверку знаков. .

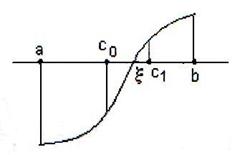
Рис. 1

Теперь корень находим на отрезке [c0, c1]. Затем находим 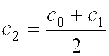и т. д. Итерационный процесс продолжается до тех пор, пока не станет меньше заданного числа : . Рабочая формула для нахождения корня имеет вид

.

Число итераций в этом методе зависит от предварительно задаваемой точности и длины отрезка [a, b] и не зависит от вида функции .

Метод медленный, всегда сходится, можно получить решение с заданной точностью, широко применяется на практике [5].

Блок-схема алгоритма метода половинного деления представлена на рис. 2, где [a, b] – отрезок, в котором находится корень уравнения;

С – корень уравнения; n – число итераций; - значение функции в соответствующей точке.

< Предыдущая		Следующая >