47. Способы задания бинарных отношений
Задание с помощью декартового произведения двух множеств
Если все первые элементы пар бинарного отношения b принадлежат множеству A, а все вторые элементы – множеству B, тогда бинарное отношение может быть задано декартовым произведением этих множеств. Если при этом окажется, что A = B, то бинарное отношение задается на множестве A. Любое бинарное отношение b на декартовом произведении множеств A и B можно превратить в бинарное отношение на некотором множестве D, если в качестве элементов множества D взять первые и вторые элементы всех упорядоченных пар бинарного отношения. В этом случае бинарное отношение можно определить как подмножество квадрата множества D: b Ì D × D.
Задание бинарного отношения указанием общего свойства пар или их перечислением
Конечное бинарное отношение может быть задано перечислением всех образующих его пар, например, b = {5 > 4; 5 > 3; 5 > 2; 4 > 3; 4 > 2; 3 > 2}.
Конечные или бесконечные бинарные отношения могут задаваться указанием общих свойств пар, входящих в эти отношения, например:
B = {(K, L) Î N × N½L является квадратом числа K, N – множество чисел натурального ряда}.
Задание бинарных отношений с помощью графов
Конечные бинарные отношения могут задаваться с помощью ориентированных графов. Пусть, например, необходимо задать бинарное отношение b Ì A × B. Тогда вершинам графа соответствуют элементы множеств A = {A1, A2, ¼, An}, B = {B1, B2, ¼, Bm}, а направленное ребро графа из вершины Ai (![]() ) в вершину Bj (
) в вершину Bj (![]() ) существует тогда и только тогда, когда упорядоченная пара (Ai, Bj) принадлежит бинарному отношению b. Если (Ai, Bj) Î b и (Bj, Ai) Î b, то вершины Ai и Bj соединяются двунаправленным ребром, а если (Ai, Ai) Î b, то в вершине Ai графа появляется петля.
) существует тогда и только тогда, когда упорядоченная пара (Ai, Bj) принадлежит бинарному отношению b. Если (Ai, Bj) Î b и (Bj, Ai) Î b, то вершины Ai и Bj соединяются двунаправленным ребром, а если (Ai, Ai) Î b, то в вершине Ai графа появляется петля.
На рис. 5.1. приведены графы полного бинарного (A), симметричного (B) и пустого (C) бинарного отношений, заданных на множестве A = {A1, A2, A3, A4}.
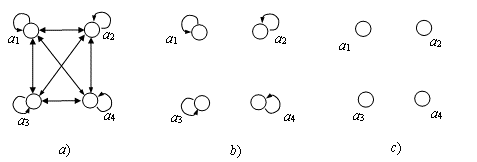
Рис. 5.1. Графы соответственно полного (a), симметричного (B) и
Пустого (с) бинарных отношений b1, b2, b3
Из рис. 5.1 a видно, что в полном бинарном отношении b1 любая пара элементов множества A принадлежит этому отношению: (Ai, Aj) Î b1, ![]() . В симметричном бинарном отношении b2 отношению принадлежат только пары равных элементов: b2 = {(A1, A1), (A2, A2), (A3, A3), (A4, A4)}. В пустом бинарном отношении b3 ни одна пара элементов множества A на принадлежит бинарному отношению.
. В симметричном бинарном отношении b2 отношению принадлежат только пары равных элементов: b2 = {(A1, A1), (A2, A2), (A3, A3), (A4, A4)}. В пустом бинарном отношении b3 ни одна пара элементов множества A на принадлежит бинарному отношению.
Задание бинарных отношений с помощью булевых матриц
Задание бинарного отношения b Ì A × B, где A = {A1, A2, ¼, An}, B = {B1, B2, ¼, Bm}, выполняется следующим образом. Строки матрицы размерами N × M нумеруются элементами A1, A2, ¼, An множества A, а столбцы – элементами множества B. Если пара элементов Ai, Bj находится в отношении b, то на пересечении I-й строки и J-го столбца записывается "1", в противном случае – записывается "0".
Булева матрица полного бинарного отношения g1, заданного на множестве A = {A1, A2, ¼, An}, является квадратной матрицей N × N, содержащей в качестве элементов только единицы. Матрица симметричного бинарного отношения g2 на множестве {A1, A2, ¼, An} также является квадратной, однако единичные элементы у нее расположены только на главной диагонали, все остальные – нули. Булева матрица пустого бинарного отношения g3 на множестве A содержит только нули.
| < Предыдущая | Следующая > |
|---|