15. Аналитическая геометрия на плоскости и в пространстве. Системы координат на плоскости и в пространстве

Полярная система координат.

Возьмем на плоскости произвольную точку и ось С выбранным масштабом. Точка называется полюсом, ось - полярной осью. - полярный радиус точки , - полярный угол. Тогда точка задается полярными координатами:

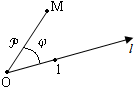
Связь полярных координат с декартовыми прямоугольными:

Совместим полюс полярной системы координат с началом декартовой прямоугольной, полярную ось - с положительным направлением оси абсцисс.

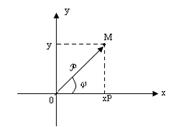
Из прямоугольного треугольника получим формулы связи декартовых и полярных координат:

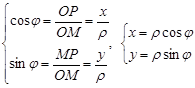
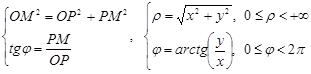
Заметим, что полярный угол определяется неоднозначно, а с точностью до периода

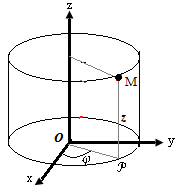
Циллиндрическая система координат.

Точка определяется тремя координатами:

- полярные координаты проекции точки на плоскость , - аппликата точки

Формулы связи декартовых координат и цилиндрических:

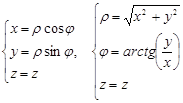
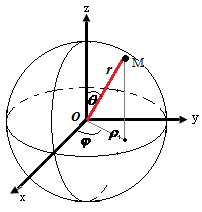
Сферическая система координат.

Точка определяется тремя координатами:

– радиус-вектор точки, - угол между проекцией радиус-вектора на плоскость Oxy и осью Ox, отсчитываемый от этой оси в положительном направлении, - Угол между радиус-вектором и осью Oz, отсчитываемый от этой оси

Сферические и декартовы координаты связаны следующими формулами:

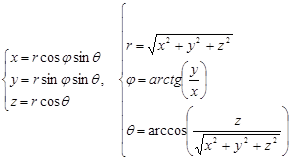
Иногда сферические координаты вводятся следующим образом: за угол принимается угол между радиус – вектором точки и плоскостью Oxy. При этом координата называется Широтой, - долготой.

В этом случае формулы связи имеют вид:

< Предыдущая		Следующая >