50. Контрольное задание №1.5
1. Пусть Г =<G, X, Y>, X = {1, 2, 3}, Y = {4, 5}, G = {<1, 4>, <1, 5>, <2, 4>, <2, 5>, <3, 4>, <3, 5>}. Проверить, является ли это соответствие полным на множестве X × Y. 2. Заданы соответствия Г =< X, Y, F>; Δ = <W, Z, P>, где X = {1, 2, 3, 4}; Y = {a, b. c, d}; F = {<1, a>, <1, c>, <1, d>, <2, b>, <2, c>, <3, a>, <3,d>, <4, b>, <4, c>}; W = {1, 3, 5, 6}; Z = {b, c, d, e}; P = {<1, b>, <1, c>, <3, b>, <3, d>, <3, e>, <5, c>,<5, d>, <6, d>}. Найти: a. Г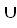
Δ; b. Г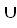Δ-1; c. Г
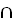Δ; d. Г-1
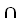Δ; e. Г\Δ; f. Г\Δ-1; g. Г-1\Δ; 3. Заданы соответствия Г =< X, Y, F>; Δ = <W, Z, P>, где X = {1, 2, 3, 4}; Y = {a, b. c, d}; F = {<1, a>, <1, c>, <1, d>, <2, b>, <2, c>, <3, a>, <3,d>, <4, b>, <4, c>}; W = {a, c, d, e}; Z = {I, II, IV, V, VI}: P = {<a, I>, <a, IV>, <a, V>, <c, II>, <c, IV>, <d, II>, <d, V>, <d, VI>, <e, I>} и произвольные множества A = {1, 2, 4}, B = {a, c, d}. Найти: a. Г •Δ; b. Δ-1•Г-1; c. Г(А); d. Г-1(В). 4. Пусть задано произвольное соответствие Г =< X, Y, F> и множества А
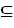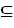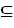Х, ВХ, СY, DY. Доказать справедливость следующих тождеств: a. Г(А
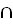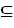В) Г(А) 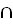Г(В); b. Г(А)\ Г(В) 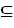Г(А\В); c. Г-1(C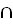D)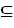 Г-1(C)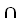Г-1(D); d. Г-1(C)\Г-1(D)
Г-1(C\D).
