14. Симметрия относительно обобщенной окружности
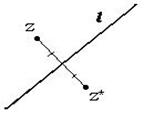 Две точки симметричны относительно прямой, если они лежат на прямой, перпендикулярной к данной прямой и расстояние от этих точек до этой прямой одинаково (см. рисунок слева).
Две точки симметричны относительно прямой, если они лежат на прямой, перпендикулярной к данной прямой и расстояние от этих точек до этой прямой одинаково (см. рисунок слева).
Две точки ![]() И
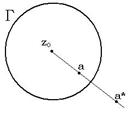
И ![]() симметричны относительно окружности радиуса
симметричны относительно окружности радиуса ![]() , если они лежат на одном луче, выходящем из центра окружности
, если они лежат на одном луче, выходящем из центра окружности ![]() и выполняется равенство:
и выполняется равенство: ![]() (см. рисунок справа). Выведем уравнение преобразования симметрии относительно окружности:
(см. рисунок справа). Выведем уравнение преобразования симметрии относительно окружности:  ;
; ![]()
В итоге получаем: 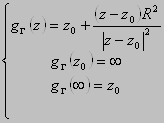 - преобразование инверсии (отражения) относительно окружности. Если
- преобразование инверсии (отражения) относительно окружности. Если ![]() , то
, то ![]() .
.
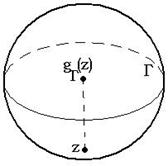
В случае, когда ![]() , на сфере Римана будет следующая картина:
, на сфере Римана будет следующая картина: ![]() . На сфере это две точки, симметричные относительно серединного сечения (см. рисунок).
. На сфере это две точки, симметричные относительно серединного сечения (см. рисунок).
Теорема Шаля: Любое ДЛО есть композиция четного числа инверсий относительно обобщенных окружностей.
Упр: Показать, что отображение ![]() можно представить композицией двух инверсий относительно окружностей.
можно представить композицией двух инверсий относительно окружностей.
| < Предыдущая | Следующая > |
|---|