05. Дуги и кривые на плоскости
Определим единичный отрезок: ![]()
Опр: Жордановой дугой в ![]() называется множество
называется множество ![]() , гомеоморфное отрезку
, гомеоморфное отрезку ![]() , т. е.
, т. е. ![]() - гомеоморфизм.
- гомеоморфизм.
Опр: Жордановой кривой в ![]() называется множество
называется множество ![]() , гомеоморфное единичной окружности
, гомеоморфное единичной окружности ![]() .
.
Теорема Жордана: Если ![]() - жорданова кривая в
- жорданова кривая в ![]() , то существует гомеоморфизм
, то существует гомеоморфизм
![]() такой, что
такой, что ![]()
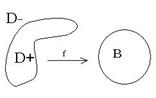
На рисунке ![]() - открытый шар, ограниченный окружностью
- открытый шар, ограниченный окружностью ![]() . Область
. Область ![]() ограницена кривой
ограницена кривой ![]() .
.
Доказательство теоремы сложное.
Опр: Область ![]() такая, что
такая, что ![]() - жорданова кривая называется Жордановой (односвязной) областью.
- жорданова кривая называется Жордановой (односвязной) областью. ![]() - Граница области.
- Граница области.
 Опр: Пусть
Опр: Пусть ![]() - область. Граница области
- область. Граница области ![]() , где
, где ![]() - жордановы кривые и
- жордановы кривые и ![]() при
при ![]() . Тогда
. Тогда ![]() называется,
называется, ![]() -Связной жордановой областью.
-Связной жордановой областью.
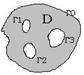
На рисунке изображен пример 4-хсвязной области.
| < Предыдущая | Следующая > |
|---|