2. Устойчивость по Ляпунову, точки покоя системы двух линейных уравнений. . Определение устойчивости
Пусть ![]() – решение уравнения
– решение уравнения ![]() , определяемое для всех
, определяемое для всех ![]() , с начальным значением
, с начальным значением ![]() . Оно называется устойчивым по Ляпунову, если для
. Оно называется устойчивым по Ляпунову, если для ![]() такое, что все решения
такое, что все решения ![]() , удовлетворяющие при
, удовлетворяющие при ![]() Условию
Условию ![]() , для всех
, для всех ![]() существуют и удовлетворяют неравенству
существуют и удовлетворяют неравенству ![]() .
.
Решение ![]() называется асимптотически устойчивым, если оно устойчиво по Ляпунову и, кроме того, существует
называется асимптотически устойчивым, если оно устойчиво по Ляпунову и, кроме того, существует
![]()
Разберем на конкретном примере свойство устойчивости решения и условия, входящие в его определение.
Рассмотрим дифференциальное уравнение Бернулли.
![]()
Легко проверить, что его общее решение будет иметь вид
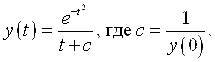
Иначе можно записать так:
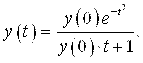
1) При начальном условии ![]()
![]()
2) При 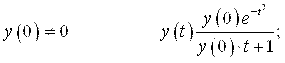
На Рис. 2.1 показаны интегральные кривые в области ![]() . Жирными линями отмечены решения, исследуемые на устойчивость.
. Жирными линями отмечены решения, исследуемые на устойчивость.

Рис. 2.1
Задача 1. Исследовать на устойчивость решение с начальным значением ![]() :
:
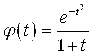 .
.
Это решение определено для всех ![]() и поэтому вопрос об устойчивости не лишен смысла.
и поэтому вопрос об устойчивости не лишен смысла.
Пусть ![]() , тогда все решения с такими начальными условиями
, тогда все решения с такими начальными условиями
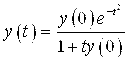
Определены для всех ![]() .
.
Составим разность
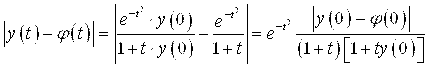
Здесь учтено, что ![]() . Из последующего вытекает, что если
. Из последующего вытекает, что если ![]() и
и ![]() , то
, то ![]() для всех
для всех ![]() .
.
Следовательно, задавшись любым ![]() , надо взять
, надо взять ![]() .
.
Тогда для всех ![]() будем иметь, что и
будем иметь, что и ![]() .
.
Более точно: 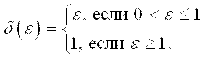
Таким образом исследуемое решение устойчиво.
Кроме того, так как ![]() .
.
Поэтому решение ![]() также и асимптотически устойчиво. Наличие асимптотической устойчивости хорошо видно на рис.2.1, так как все решения с начальными условиями
также и асимптотически устойчиво. Наличие асимптотической устойчивости хорошо видно на рис.2.1, так как все решения с начальными условиями ![]() асимптотически приближаются к
асимптотически приближаются к ![]() .
.
Задача 2. Для того же уравнения исследовать на устойчивость тривиальное решение ![]() .
.
Возвратимся к формуле
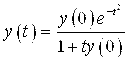
Легко заметить, что при ![]() решение
решение ![]() определено не для всех
определено не для всех ![]() , так как при
, так как при 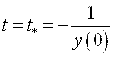 знаменатель обращается в нуль, поэтому при
знаменатель обращается в нуль, поэтому при ![]() .
.
Так как отрицательное значение ![]() можно взять сколь угодно близким к
можно взять сколь угодно близким к ![]() , то заключаем, что не существует окрестность точки
, то заключаем, что не существует окрестность точки ![]() , для которой все решения уравнения существовали бы для всех
, для которой все решения уравнения существовали бы для всех ![]() .
.
Решение ![]() неустойчиво.
неустойчиво.
Ра рис. 2.1 это можно наглядно проиллюстрировать: решения с отрицательными начальными значениями, начинающиеся сколь угодно близко от ![]() , неограниченно удаляются от
, неограниченно удаляются от ![]() , а
, а ![]() неограниченно возрастает при
неограниченно возрастает при  .
.
| < Предыдущая | Следующая > |
|---|