06. Операции над множествами
Продолжая описание методов получения новых множеств из уже существующих, мы опишем два метода, при помощи которых из двух множеств строится новое множество. Эти так называемые операции над множествами в некоторых отношениях аналогичны операциям сложения и умножения целых чисел. Объединение. (соединение, сумма) множеств A и В (обозначается через A![]() В; A
В; A![]() В читается как «объединение А и В» или «A чашка В») есть множество всех предметов, которые являются элементами множества A или В; иными словами,
В читается как «объединение А и В» или «A чашка В») есть множество всех предметов, которые являются элементами множества A или В; иными словами,
А![]() В = {х| х
В = {х| х![]() А Или X
А Или X![]() В}.
В}.
Здесь подразумевается неисключающий смысл слова «или»
Таким образом, по определению Х![]() A
A![]() B тогда и только тогда, когда Х Есть элемент хотя бы одного из множеств A и B. Например,
B тогда и только тогда, когда Х Есть элемент хотя бы одного из множеств A и B. Например,
{1, 2, 3}![]() {1, 3, 4} = {1, 2, 3, 4}.
{1, 3, 4} = {1, 2, 3, 4}.
Пересечение (произведение) множеств A и B(обозначается через A![]() В; А
В; А![]() В читается как «пересечение А и В» или «A крышка B») есть множество всех предметов, являющихся элементами обоих множеств А и В; иными словами:
В читается как «пересечение А и В» или «A крышка B») есть множество всех предметов, являющихся элементами обоих множеств А и В; иными словами:
А![]() В = {х| х
В = {х| х![]() А И X
А И X![]() В}.
В}.
Таким образом, по определению Х![]() А
А![]() В тогда и только тогда, когда X
В тогда и только тогда, когда X![]() A и Х
A и Х![]() В. Например,
В. Например,
{1, 2, 3}![]() {1, 3, 4}-{1, 3}.
{1, 3, 4}-{1, 3}.
Предоставляем читателю в качестве упражнения доказать, что для всякой пары множеств А и В имеют место следующие включения:
ɸ![]() А
А![]() В
В![]() А
А![]() А
А![]() В
В
Два множества А и В называются Непересекающимися (или Расчлененными), если А![]() В= ɸ, и Пересекающимися, если А
В= ɸ, и Пересекающимися, если А![]() В≠ ɸ. Система множеств называется Расчлененной, если любая пара ее различных элементов является непересекающейся. Разбиением множества X мы будем называть такую расчлененную систему U непустых и различных подмножеств множества Х, что каждый элемент множества X Является в то же время элементом некоторого (а следовательно, в точности одного) элемента системы U. Например, {{1, 2}, {3}, [4, 5}} Есть разбиение множества {1, 2, 3, 4, 5}.
В≠ ɸ. Система множеств называется Расчлененной, если любая пара ее различных элементов является непересекающейся. Разбиением множества X мы будем называть такую расчлененную систему U непустых и различных подмножеств множества Х, что каждый элемент множества X Является в то же время элементом некоторого (а следовательно, в точности одного) элемента системы U. Например, {{1, 2}, {3}, [4, 5}} Есть разбиение множества {1, 2, 3, 4, 5}.
Следующая операция — операция перехода к дополнению — позволяет образовать новое множество из одного ранее существовавшего множества. Абсолютное дополнение множества А (обозначается через Ā) — это не что иное, как множество {х|х![]() А}. Относительное дополнение множества А до множества X — это множество Х
А}. Относительное дополнение множества А до множества X — это множество Х![]() Ā; оно обычно обозначается через Х - А, что читается как «Х минус А». Таким образом, Х - А есть сокращение для
Ā; оно обычно обозначается через Х - А, что читается как «Х минус А». Таким образом, Х - А есть сокращение для
X![]() X\X
X\X![]() A},
A},
Т. е. для множества тех элементов множества X, которые не являются элементами множества А.
Симметрическая разность множеств А и В, обозначаемая через А+В, определяется следующим образом:
А+В=(А-В)![]() (В-А).
(В-А).
Эта операция коммутативна [А+B=В+А] и ассоциативна [(А+В)+С=А+(В+С)]. Кроме того, А+А=ɸ И А+ɸ=А. Доказательства этих утверждений предоставляются читателю.
Если все рассматриваемые в ходе какого-либо рассуждения множества являются подмножествами некоторого множества U, то это множество U называют Универсальным множеством (для этого рассуждения). Например, для элементарной арифметики универсальным множеством служит Z, а для аналитической геометрии плоскости — множество всех упорядоченных пар действительных чисел. Для графической иллюстрации отношений, которые могут иметь место между подмножествами какого-либо универсального множества U, часто используют так называемые Диаграммы Венна. Диаграмма Венна представляет собой схематическое изображение множеств в виде точечных множеств: универсальное множество U изображается множеством точек некоторого прямоугольника, а его подмножество А — в виде круга или какой-нибудь другой простой области внутри этого прямоугольника. Дополнение множества А (до U), которое мы можем, не опасаясь двусмысленности, обозначать через Ā, изображается в таком случае той частью прямоугольника, которая лежит за пределами круга, изображающего А (рис.1). Если изобразить таким образом какие-нибудь множества А и В, являющиеся подмножествами множества U, то множества А![]() В и А
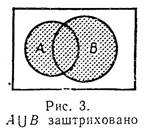
В и А![]() В изображаются областями, заштрихованными, соответственно, на рисунках 2 и 3. Непересекающиеся множества изображаются неперекрывающимися областями, а включение множеств соответствует тому обстоятельству, что одна из областей на диаграмме Венна целиком лежит внутри другой. Построение диаграммы Венна для сложного выражения, составленного из нескольких множеств посредством объединения, пересечения, дополнения и включения, осуществляется комбинированием описанных способов построения диаграмм для этих составных частей. Диаграммы Венна применяются главным образом для упрощения некоторого данного сложного выражения или совокупности условий на подмножества универсального множества. Ниже мы приведем три простых примера
В изображаются областями, заштрихованными, соответственно, на рисунках 2 и 3. Непересекающиеся множества изображаются неперекрывающимися областями, а включение множеств соответствует тому обстоятельству, что одна из областей на диаграмме Венна целиком лежит внутри другой. Построение диаграммы Венна для сложного выражения, составленного из нескольких множеств посредством объединения, пересечения, дополнения и включения, осуществляется комбинированием описанных способов построения диаграмм для этих составных частей. Диаграммы Венна применяются главным образом для упрощения некоторого данного сложного выражения или совокупности условий на подмножества универсального множества. Ниже мы приведем три простых примера


![]() заштриховано А
заштриховано А![]() В заштриховано A
В заштриховано A![]() B заштриховано
B заштриховано
Такого рода. Во многих случаях такие диаграммы оказываются недостаточными, но их использование все же может помочь при освоении алгебраического подхода, развиваемого в следующем параграфе.
Примеры
1. Пусть А и В — два таких множества, что А-В=В-А= ɸ.
Можно ли выразить отношение между А И В более простым образом?



Поскольку А-В= ɸ означает, что А![]()
![]() =ɸ, области, представляющие А и
=ɸ, области, представляющие А и ![]() на диаграмме Венна (рис. 4), не перекрываются. Очевидно,
на диаграмме Венна (рис. 4), не перекрываются. Очевидно,
![]() =В, так что мы получаем А
=В, так что мы получаем А![]() В (рис. 5). И обратно, если А
В (рис. 5). И обратно, если А![]() В, то, очевидно, А-В=ɸ. Мы приходим к выводу, что А-В =ɸ равносильно А
В, то, очевидно, А-В=ɸ. Мы приходим к выводу, что А-В =ɸ равносильно А![]() В. Поменяв ролями А и В, мы получим, что В-А=ɸ равносильно В
В. Поменяв ролями А и В, мы получим, что В-А=ɸ равносильно В![]() А. Таким образом, заданные отношения между А и В равносильны тому, что А
А. Таким образом, заданные отношения между А и В равносильны тому, что А![]() В и B
В и B![]() A, т. е. А = В.
A, т. е. А = В.
2. Рассмотрим вопрос, можно ли указать три таких подмножества А, В и С универсального множества U, для которых одновременно имели бы место следующие соотношения:
С ≠ ɸ, А ![]() В ≠ ɸ, (А
В ≠ ɸ, (А ![]() В)-С= ɸ.
В)-С= ɸ.
A B![]() = ɸ
= ɸ

Таб.1
Из второго условия вытекает, что А и В пересекаются, из чего, кстати, следует, что оба они непусты. Согласно примеру 1 четвертое условие равносильно тому, что A![]() В
В![]() С, из чего видно, что первое условие является излишним. С помощью диаграммы Венна легко убедиться, что А и С Пересекаются, т. е. что второе и четвертое условия противоречат третьему. Следовательно, множеств, одновременно удовлетворяющих всем приведенным условиям, не существует.
С, из чего видно, что первое условие является излишним. С помощью диаграммы Венна легко убедиться, что А и С Пересекаются, т. е. что второе и четвертое условия противоречат третьему. Следовательно, множеств, одновременно удовлетворяющих всем приведенным условиям, не существует.
3. Пусть F, G и L — такие подмножества множества U, что
F![]() G, G
G, G ![]() L
L![]() F, L
F, L![]() F=ɸ.
F=ɸ.
Можно ли на самом деле найти такие множества F, G и L, которые удовлетворяли бы этой совокупности условий? Диаграмма Венна (рис. 6) иллюстрирует только первое и третье условия. Но теперь из второго условия следует, что L И G Не могут пересекаться, так что G![]() L=ɸ. С другой стороны, если F
L=ɸ. С другой стороны, если F![]() G и G
G и G![]() L=ɸ, то выполняются все заданные условия. Таким Образом, данная система условий может быть сведена к более простой: F
L=ɸ, то выполняются все заданные условия. Таким Образом, данная система условий может быть сведена к более простой: F![]() G и G
G и G![]() L=ɸ.
L=ɸ.
Упражнения
Замечание. В упражнениях 1 — 8 надо обойтись без использования диаграмм Венна.
1. Доказать, что для любых множеств А И В Верно ɸ ![]() А
А![]() В
В![]() А
А![]() В.
В.
2. Пусть универсальным множеством служит Z и пусть
A={X![]() Z} для некоторого положительного целого числа У х = 2у},
Z} для некоторого положительного целого числа У х = 2у},
В = {х![]() Z} | для некоторого положительного целого числа У х = 2у — 1}.
Z} | для некоторого положительного целого числа У х = 2у — 1}.
C = {X![]() Z| X<10}.
Z| X<10}.
Опишите множества ![]() ,
, ![]() ,
, ![]() , А —
, А — ![]() и C - (А
и C - (А![]() В) словесно или с помощью определяющего свойства.
В) словесно или с помощью определяющего свойства.
3. Рассмотрим следующие подмножества множества целых положительных чисел Z +:
A = {X![]() Z+| Для некоторого целого числа у х = 2у},
Z+| Для некоторого целого числа у х = 2у},
B = {X![]() Z+| для некоторого целого числа у х = 2у+1},
Z+| для некоторого целого числа у х = 2у+1},
С = {X![]() Z+| Для некоторого целого числа у х = 3у}.
Z+| Для некоторого целого числа у х = 3у}.
(а) Опишите А![]() С, В
С, В![]() С и В — С.
С и В — С.
(b) Проверьте, что А![]() (В
(В![]() С) = (А
С) = (А![]() В)
В) ![]() (А
(А![]() С).
С).
4. Пусть A — произвольное множество. Что представляют собой следующие множества: А![]() ɸ, А
ɸ, А![]() ɸ, А — ɸ, А — А, ɸ — А?
ɸ, А — ɸ, А — А, ɸ — А?
5. Определите: ɸ![]() {ɸ}, {ɸ}
{ɸ}, {ɸ}![]() {ɸ}, {Ф, {Ф}} - ɸ, {ɸ, {ɸ}} — {ɸ}, {ɸ, {ɸ}} - {{ɸ}}.
{ɸ}, {Ф, {Ф}} - ɸ, {ɸ, {ɸ}} — {ɸ}, {ɸ, {ɸ}} - {{ɸ}}.
6. Пусть А и В — подмножества множества U. Покажите, что для каждой приведенной ниже системы соотношений (а), (B) И (с) из справедливости одного соотношения системы вытекает справедливость всех других соотношений данной системы:
(a) А![]() В,
В, ![]()
![]()
![]() , A
, A![]() В = В, А
В = В, А![]() В = А;
В = А;
(b) А![]() В = ɸ, А
В = ɸ, А![]()
![]() , B
, B![]() ;
;
(c) A![]() B = U,
B = U, ![]()
![]() B, В
B, В![]()
![]() .
.
7. Докажите, что для произвольных множеств А, В и С
(А![]() В)
В) ![]() С = A
С = A![]() (B
(B![]() С) равносильно C
С) равносильно C![]() A.
A.
8. Докажите, что для произвольных множеств А, В и С
(A — B) —С = (A —С) — (В — С).
9. (а) Постройте диаграмму Венна, соответствующую симметрической разности А - В множеств А и В;
(b) с помощью диаграммы Венна покажите коммутативность и ассоциативность операции симметрической разности;
(c) покажите, что для любого множества А А — А = ɸ, A+ɸ = A.
10. На диаграмме Венна для подмножеств А, В и С универсального множества U прямоугольник, соответствующий U, разбивается, вообще говоря, на восемь неперекрывающихся областей. Укажите, какие комбинации множеств A, В и С Соответствуют каждой из этих областей.
11. С помощью диаграмм Венна исследуйте вопрос о справедливости каждого из следующих рассуждений:
(a) Если А, В И С — такие подмножества множества U, Что A![]() B
B![]()
![]() И A
И A![]() C
C![]() B, то A
B, то A![]() С = ɸ,
С = ɸ,
(B) Если A, В И С — такие такие подмножества множества U, Что A![]()
![]() И B
И B![]()
1.5. Алгебра множеств
Если мы захотим приняться за рассмотрение белее сложных вопросов, касающихся различных соотношений между множествами, нежели те, которых мы касались выше, то мы сразу же ощутим необходимость
В более систематизированных методах обращения с множествами, относящихся к включению, объединению, пересечению и дополнению.
Иначе говоря, то, что ниже будет естественным образом названо «алгеброй множеств» — это не что иное, как дальнейшее развитие основных свойств операций ![]() ,
, ![]() ,
, ![]() И
И ![]() , и связей между ними. Можно сказать, что алгебра множеств представляет собой теоретико-множественный аналог обычной алгебры действительных чисел, исходящей из свойств операций +, . и ≤ и их взаимосвязей. Алгебра множеств представляет собой совокупность тождеств-равенств, справедливых независимо от того, каково универсальное множество U и какие именно конкретные подмножества множества U Обозначаются входящими в эти равенства буквами (отличными от U и ɸ).
, и связей между ними. Можно сказать, что алгебра множеств представляет собой теоретико-множественный аналог обычной алгебры действительных чисел, исходящей из свойств операций +, . и ≤ и их взаимосвязей. Алгебра множеств представляет собой совокупность тождеств-равенств, справедливых независимо от того, каково универсальное множество U и какие именно конкретные подмножества множества U Обозначаются входящими в эти равенства буквами (отличными от U и ɸ).
Первый наш результат устанавливает основные свойства объединения и пересечения. Ради единообразия все эти свойства будут сформулированы для подмножеств универсального множества U. Однако для некоторых из этих свойств упомянутое ограничение является совершенно несущественным, что видно из приводимых ниже доказательств.
Теорема 1.1. Для любых подмножеств А, В и С универсального множества U следующие равенства являются тождествами (A здесь используется в качестве сокращения для U — A):
1. A![]() B (B
B (B![]() C) = (A
C) = (A![]() B)
B) ![]() C. 1´. A
C. 1´. A![]() B (B
B (B![]() C) = (A
C) = (A![]() B)
B)![]() C.
C.
2. A![]() B = B
B = B![]() A. 2´. A
A. 2´. A![]() B = B
B = B![]() A.
A.
3. A![]() (B
(B![]() C) = (A
C) = (A![]() B)
B) ![]() (A
(A![]() C). 3´. A
C). 3´. A![]() (B
(B![]() C) = (A
C) = (A![]() B)
B) ![]() (A
(A![]() C).
C).
4. A![]() ɸ = A 4'. A
ɸ = A 4'. A![]() U = A.
U = A.
5. A![]()
![]() = U. 5´. A
= U. 5´. A![]()
![]() = ɸ.
= ɸ.
Доказательство. Справедливость каждого из этих утверждений можно проверить, показав, что множество, стоящее по одну сторону от знака равенства, включено в множество, стоящее по другую сторону от этого знака равенства. В качестве примера докажем тождество 3.
(a) Доказательство того, что A![]() (B
(B![]() C)
C)![]() (A
(A![]() B)
B) ![]() (A
(A![]() C). Пусть X
C). Пусть X![]() A
A![]() (B
(B![]() C). Тогда X
C). Тогда X![]() A или X
A или X![]() B
B![]() C. Если X
C. Если X![]() A, то X
A, то X![]() A
A![]() B и X
B и X![]() A
A![]() C, а, следовательно, Х есть элемент пересечения этих множеств. Если X
C, а, следовательно, Х есть элемент пересечения этих множеств. Если X![]() B
B![]() C, то X
C, то X![]() B и X
B и X![]() C. Следовательно, X
C. Следовательно, X![]() A
A![]() B и X
B и X![]() A
A![]() C, так что и в этом случае Х есть элемент их пересечения.
C, так что и в этом случае Х есть элемент их пересечения.
(b) Доказательство того, что (A![]() B)
B)![]() (A
(A![]() C)
C) ![]() A
A![]() (B
(B![]() C). Пусть X
C). Пусть X![]() (A
(A![]() B)
B)![]() (A
(A![]() C). Тогда X
C). Тогда X![]() (A
(A![]() B) и X
B) и X![]() (A
(A![]() C). Следовательно, X
C). Следовательно, X![]() A, или же X
A, или же X![]() B и X
B и X![]() C. Из этого и вытекает, что X
C. Из этого и вытекает, что X![]() (A
(A![]() B)
B)![]() (A
(A![]() C).
C).
Тождества 1 и 1´ называют ассоциативными законами, соответственно, для объединения и пересечения, а тождества 2 и 2' — коммутативными законами для этих операций. Тождества 3 и 3'—это дистрибутивные законы для этих операций. В этом пункте нарушается аналогия, имеющая место между свойствами объединения и пересечения множеств, с одной стороны, и, соответственно, сложения и умножения чисел — с другой. 3' в точности соответствует дистрибутивному закону арифметики. Расхождение проявляется в тождестве 3, для которого в арифметике нет аналога.
Согласно ассоциативному закону (тождество 1), два множества, которые можно образовать с помощью операции объединения, исходя из множеств А, В и С, взятых в определенном порядке, равны. Условимся обозначать это единственное множество через A![]() В
В![]() С. Ассоциативный закон утверждает, что не играет роли, как расставить скобки в этом выражении. При помощи математической индукции этот результат можно обобщить следующим образом. Все множества, получаемые с помощью операции объединения из заданных множеств A1, A2, ..., An взятых в фиксированном порядке, равны друг другу. Множество, получаемое таким способом из A1, A2, ..., An, мы будем обозначать через
С. Ассоциативный закон утверждает, что не играет роли, как расставить скобки в этом выражении. При помощи математической индукции этот результат можно обобщить следующим образом. Все множества, получаемые с помощью операции объединения из заданных множеств A1, A2, ..., An взятых в фиксированном порядке, равны друг другу. Множество, получаемое таким способом из A1, A2, ..., An, мы будем обозначать через
A1 ![]() A2
A2 ![]() ...,
..., ![]() An
An
В силу тождества 1´ соответствующее обобщение справедливо и для операции пересечения. Эти общие ассоциативные законы позволяют нам установить общие коммутативные законы: если 1´, 2´, ,n´ суть числа 1, 2, .... n, взятые в произвольном порядке, то
A1 ![]() A2
A2 ![]() ...,
..., ![]() An = A1´
An = A1´ ![]() A2´
A2´ ![]() ...,
..., ![]() An´.
An´.
То же можно сказать и об общих дистрибутивных законах:
A ![]() (B1
(B1 ![]() B2
B2 ![]() ……
…… ![]() Bn) = (A
Bn) = (A ![]() B1)
B1) ![]() (A
(A ![]() B2)
B2) ![]() …..
….. ![]() (A
(A ![]() Bn),
Bn),
A ![]() (B1
(B1 ![]() B2
B2 ![]() ……
…… ![]() Bn) = (A
Bn) = (A ![]() B1)
B1) ![]() (A
(A ![]() B2)
B2) ![]() …..
….. ![]() (A
(A ![]() Bn).
Bn).
Законы эти также могут быть доказаны по индукции.
Подробные доказательства дальнейших свойств объединения и пересечения не требуют никаких ссылок на отношение принадлежности — ти свойства непосредственно следуют из тех, которые устанавливаются в теореме 1.1. Это относится, в частности, и к тем свойствам, которые фигурируют в следующей теореме. Это обстоятельство можно расценивать как источник «аксиоматического подхода» к алгебре множеств, развиваемого ниже, в главе IV. Подход этот основан на том, что любая теорема алгебры множеств выводима из 1 — 5 и 1´ — 5´.
Указанные десять свойств позволяют сделать и другой интересный вывод. В теореме 1.1 эти свойства фигурируют попарно таким образом, что каждый член любой пары получается из другого члена одновременной взаимной заменой ![]() и
и ![]() , ɸ и U. Равенство (или выражение, или утверждение) алгебры множеств, полученное из другого равенства (соответственно, выражения или утверждения) заменой всех вхождений
, ɸ и U. Равенство (или выражение, или утверждение) алгебры множеств, полученное из другого равенства (соответственно, выражения или утверждения) заменой всех вхождений ![]() на
на ![]() ,
, ![]() на
на ![]() , ɸ на U и U на ɸ, называют двойственным исходному. Мы утверждаем, что предложение, двойственное любой теореме алгебры множеств, сформулированной в терминах
, ɸ на U и U на ɸ, называют двойственным исходному. Мы утверждаем, что предложение, двойственное любой теореме алгебры множеств, сформулированной в терминах ![]() ,
, ![]() и
и ![]() , для доказательства которой можно обойтись лишь тождествами 1 — 5 и, также является теоремой. В самом деле, допустим, что доказательство исходной теоремы представлено в виде последовательности шагов, а рядом с каждым шагом записано его обоснование. По предположению каждое такое обоснование является одним из тождеств 1 — 5, 1´ — 5´ или условием теоремы. Заменим теперь каждое тождество и соотношение, встречающееся в доказательстве и обосновании, двойственным ему. Поскольку тождество, двойственное каждому из тождеств 1 — 5, 1´ — 5´, снова является одним из этих тождеств, а утверждение, двойственное посылке исходной теоремы, является посылкой ноеой теоремы, результат замены каждого шага обоснования в доказательстве исходной теоремы может служить обоснованием соответствующего шага новой последовательности, которая, следовательно, будет являться доказательством. Таким образом, последняя строка новой последовательности является теоремой, двойственной исходной теореме. Согласившись, что любая теорема алгебры множеств может быть выведена из условий 1 — 5 и 1´ — 5´, мы приходим к принципу двойственности для алгебры множеств: для любой теоремы Т, формулируемой в терминах
, для доказательства которой можно обойтись лишь тождествами 1 — 5 и, также является теоремой. В самом деле, допустим, что доказательство исходной теоремы представлено в виде последовательности шагов, а рядом с каждым шагом записано его обоснование. По предположению каждое такое обоснование является одним из тождеств 1 — 5, 1´ — 5´ или условием теоремы. Заменим теперь каждое тождество и соотношение, встречающееся в доказательстве и обосновании, двойственным ему. Поскольку тождество, двойственное каждому из тождеств 1 — 5, 1´ — 5´, снова является одним из этих тождеств, а утверждение, двойственное посылке исходной теоремы, является посылкой ноеой теоремы, результат замены каждого шага обоснования в доказательстве исходной теоремы может служить обоснованием соответствующего шага новой последовательности, которая, следовательно, будет являться доказательством. Таким образом, последняя строка новой последовательности является теоремой, двойственной исходной теореме. Согласившись, что любая теорема алгебры множеств может быть выведена из условий 1 — 5 и 1´ — 5´, мы приходим к принципу двойственности для алгебры множеств: для любой теоремы Т, формулируемой в терминах ![]() ,
, ![]() и
и ![]() , двойственное ей предложение также является теоремой. Из этого принципа, например, получается, что если какое-нибудь утверждение следующей теоремы непосредственно вытекает из теоремы 1.1, то соответствующее ему (т. е. находящееся в паре с тем же номером) утверждение также в силу двойственности вытекает из теоремы 1.1. Читатель сам сможет убедиться, что все утверждения теоремы 1.2 истинны, используя определения для
, двойственное ей предложение также является теоремой. Из этого принципа, например, получается, что если какое-нибудь утверждение следующей теоремы непосредственно вытекает из теоремы 1.1, то соответствующее ему (т. е. находящееся в паре с тем же номером) утверждение также в силу двойственности вытекает из теоремы 1.1. Читатель сам сможет убедиться, что все утверждения теоремы 1.2 истинны, используя определения для ![]() ,
, ![]() и
и ![]() в терминах отношения принадлежности. После этого стоило бы попытаться вывести некоторые из этих утверждений прямо из теоремы 1.1, т. е. без какой бы то ни было апелляции к определению отношения принадлежности. Некоторые примеры такого рода читатель найдет ниже, в доказательстве теоремы 4.1.
в терминах отношения принадлежности. После этого стоило бы попытаться вывести некоторые из этих утверждений прямо из теоремы 1.1, т. е. без какой бы то ни было апелляции к определению отношения принадлежности. Некоторые примеры такого рода читатель найдет ниже, в доказательстве теоремы 4.1.
Теорема 1.2. Для произвольных подмножеств А и В множества U Справедливы следующие утверждения (![]() здесь служит сокращением для U – A).
здесь служит сокращением для U – A).
6. Если для всех A A![]() B = A, 6´. Если для всех A A
B = A, 6´. Если для всех A A![]() B = A,
B = A,
то B = ɸ. то B = U.
7. 7'. Если A ![]() B = U И A
B = U И A ![]() B = ɸ, То B =
B = ɸ, То B = ![]() .
.
8.8´. ![]() . = A.
. = A.
9. ɸ = U. 9´. ![]() = ɸ
= ɸ
10. A ![]() A = A. 10´. A
A = A. 10´. A ![]() A = A
A = A
11. A ![]() U= U. 11´. A
U= U. 11´. A ![]() ɸ = ɸ.
ɸ = ɸ.
12. A ![]() (А
(А ![]() В) = А. 12´. А
В) = А. 12´. А ![]() (А
(А ![]() В) = А.
В) = А.
13. ![]() =
= ![]()
![]()
![]() . 13. ´
. 13. ´![]() .=
.= ![]()
![]()
![]()
Некоторые из тождеств теоремы 1.2 известны под специальными именами. Так, 10 и 10´ — это законы идемпотентности, 12 и 12´ — законы поглощения, 13 и 13´ — законы де Моргана. Каждое из тождеств 7, 7´ и 8, 8´ занумеровано дважды, чтобы подчеркнуть, что каждое из них не меняется при преобразовании, переводящем его в двойственное; такие формулы называют самодвойственными. Заметим, что 7, 7´ утверждает, что каждое множество имеет единственное дополнение.
По поводу следующей теоремы требуется пояснение. Утверждение вида «Предложения R1 R2, ..., RK попарно эквивалентны» означает: «Для любых I и J Ri эквивалентно Rj», что, в свою очередь, справедливо в том и только в том случае, когда R1 влечет R2, R2 влечет R3, ..., R K-1Влечет RK, R K влечет R1. Содержанием теоремы является то, что отношение включения множеств может быть определено в терминах объединения, а также в терминах пересечения.
Теорема 1.3. Следующие предложения о произвольных множествах А и В Попарно эквивалентны:
(I) A![]() B;
B;
(II) A ![]() B = A;
B = A;
(III) A ![]() B = B.
B = B.
Доказательство. (I) влечет (II). Пусть A![]() B. Поскольку для всех А и В A
B. Поскольку для всех А и В A![]() B
B![]() A, нам достаточно доказать, что A
A, нам достаточно доказать, что A![]() A
A![]() B. Но если X
B. Но если X![]() A, то X
A, то X![]() B и, следовательно, X
B и, следовательно, X![]() A
A![]() B. Значит, A
B. Значит, A![]() A
A![]() B.
B.
(II) влечет (III). Пусть A![]() B = A. Тогда A
B = A. Тогда A![]() B = (A
B = (A![]() B)
B)![]() B = (A
B = (A![]() B)
B)![]() (B
(B![]() B) = (A
B) = (A![]() B)
B)![]() B = B.
B = B.
(III) влечет (I). Пусть A![]() B = B. Но из этого тождества и тождества A
B = B. Но из этого тождества и тождества A![]() A
A![]() B следует A
B следует A![]() B.
B.
Принцип двойственности в том виде, как он был сформулирован выше, не приложим непосредственно к выражениям, содержащим знаки ![]() или
или ![]() . На вычитание этот принцип может быть распространен использованием несокращенной формы, а именно A
. На вычитание этот принцип может быть распространен использованием несокращенной формы, а именно A![]()
![]() вместо А — В. Точно так же в силу теоремы 1.3 А
вместо А — В. Точно так же в силу теоремы 1.3 А![]() В можно заменить на A
В можно заменить на A![]() B = А (или А
B = А (или А![]() В = В). А еще лучше будет сказать, что, поскольку двойственным к A
В = В). А еще лучше будет сказать, что, поскольку двойственным к A![]() B = А является соотношение A
B = А является соотношение A![]() B = А, эквивалентное А
B = А, эквивалентное А![]() В, то принцип двойственности может быть расширен на тот случай, когда в выражение входит символ включения, распоряжением, чтобы при переходе к двойственному выражению все знаки
В, то принцип двойственности может быть расширен на тот случай, когда в выражение входит символ включения, распоряжением, чтобы при переходе к двойственному выражению все знаки ![]() (
(![]() ) заменялись на
) заменялись на ![]() (соответственно,
(соответственно, ![]() ) и обратно.
) и обратно.
| < Предыдущая | Следующая > |
|---|