04. Тема 2. Стохастический эксперимент. Случайные события. Операции над случайными событиями
Литература: [1, c.23-26], [2,c.23], [4, c.16-25], [6, c.9-16], [6, c. 15-23], [8, с.3-10], [9, с.7-12], [10, с. 10-15].
Занятие 2 предназначено для овладения исходными понятиями теории вероятностей, которыми являются понятия стохастического эксперимента, случайного события, алгебры случайных событий и вероятности случайных событий. В основе теоретико-множественного метода изложения теории вероятностей лежит предположение, что рассматриваемому стохастическому эксперименту поставлено в соответствие некоторое множество W, точки которого изображают наиболее полную информацию о возможных результатах в данном эксперименте. Множество W называют пространством описаний элементарных случайных событий, а его точки – описаниями элементарных случайных событий (описаниями элементарных исходов), если это множество состоит из взаимоисключающих исходов эксперимента, а каждый интересующий нас результат эксперимента может быть однозначно описан с помощью элементов этого множества. С множеством W связывают некоторую систему подмножеств ![]() , обладающую определёнными свойствами, называемую алгеброй подмножеств множества W. Любое множество из
, обладающую определёнными свойствами, называемую алгеброй подмножеств множества W. Любое множество из ![]() называется случайным событием. Раз событие формально есть подмножество множества W, то над событиями выполняются те же операции, что и над множествами.
называется случайным событием. Раз событие формально есть подмножество множества W, то над событиями выполняются те же операции, что и над множествами.
Объединением ![]() событий
событий ![]() и
и ![]() называется событие, состоящее из тех элементарных событий, которые входят в событие
называется событие, состоящее из тех элементарных событий, которые входят в событие ![]() или в событие
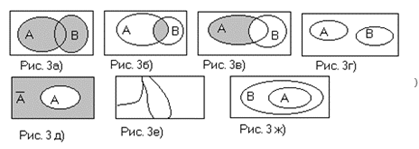
или в событие ![]() , или и в то и другое одновременно (рис. 3 а ). Другими словами, событие
, или и в то и другое одновременно (рис. 3 а ). Другими словами, событие ![]() наступает тогда и только тогда, когда наступает хотя бы одно из событий
наступает тогда и только тогда, когда наступает хотя бы одно из событий ![]() или
или ![]() .
.
Пересечением ![]() событий
событий ![]() и
и ![]() называется событие, состоящее из тех элементарных событий, которые входят и в
называется событие, состоящее из тех элементарных событий, которые входят и в ![]() и в
и в ![]() одновременно (рис. 3 б ). Т. е. событие
одновременно (рис. 3 б ). Т. е. событие ![]() наступает тогда и только тогда, когда наступают одновременно и
наступает тогда и только тогда, когда наступают одновременно и ![]() и
и ![]() .
.
Разностью ![]()
![]() называется событие, состоящее из тех элементарных событий, которые входят в
называется событие, состоящее из тех элементарных событий, которые входят в ![]() и не входят в
и не входят в ![]() (рис. 3 в). Т. е. событие
(рис. 3 в). Т. е. событие ![]()
![]() наступает в случае, если наступает
наступает в случае, если наступает ![]() и не наступает
и не наступает ![]() .
.
Множество W называется Достоверным Событием. Достоверное событие всегда наступает в результате однократного воспроизведения случайного эксперимента. Пустое множество Æ Называется Невозможным Событием. Невозможное событие никогда не наступает в результате воспроизведения эксперимента.
События ![]() и
и ![]() называются Несовместными, если
называются Несовместными, если ![]() (рис. 3 г ), т. е.
(рис. 3 г ), т. е. ![]() и
и ![]() никогда не наблюдаются одновременно. В том случае, когда
никогда не наблюдаются одновременно. В том случае, когда ![]() , иногда пишут
, иногда пишут ![]() вместо
вместо ![]() . Событие
. Событие ![]() называется Противоположным событию
называется Противоположным событию ![]() , если
, если ![]() и
и ![]() (рис. 3 д). События
(рис. 3 д). События ![]() образуют Полную группу попарно несовместных событий, если
образуют Полную группу попарно несовместных событий, если ![]() и
и ![]() (рис. 3 е ).
(рис. 3 е ).
Если каждое появление события ![]() сопровождается появлением
сопровождается появлением ![]() , то пишут
, то пишут ![]() и говорят, что
и говорят, что ![]() влечет за собой
влечет за собой ![]() . Если
. Если ![]() , то каждое элементарное событие, входящее в
, то каждое элементарное событие, входящее в ![]() , содержится в событии
, содержится в событии ![]() (рис. 3 ж).
(рис. 3 ж).
Для различных стохастических экспериментов, описанных в задачах этих занятий, необходимо построить множество W, выяснить, как случайному событию ![]() , связанному с данным экспериментом, ставится в соответствие подмножество пространства описаний элементарных исходов W, какая взаимосвязь результатов операций над случайными событиями и результатов соответствующих операций над подмножествами пространства W. Часть задач требует выполнения некоторых преобразований с использованием законов для операций над событиями:
, связанному с данным экспериментом, ставится в соответствие подмножество пространства описаний элементарных исходов W, какая взаимосвязь результатов операций над случайными событиями и результатов соответствующих операций над подмножествами пространства W. Часть задач требует выполнения некоторых преобразований с использованием законов для операций над событиями:
А) Ассоциативный закон (сочетательный)
![]() Б) Коммутативный закон (переместительный)
Б) Коммутативный закон (переместительный)
![]()
В) два Дистрибутивных (распределительных) закона
![]()
![]()
Г) связь операции пересечения и операции разности двух событий
![]() ;
;
Д) Закон де Моргана
![]()
| < Предыдущая | Следующая > |
|---|