4.2. Метод деления отрезка пополам

Метод деления отрезка пополам является простейшим последовательным  методом минимизации. Он позволяет для любой функции F(X)Q[A, B] построить последовательность вложенных отрезков  [A, B]  [A1,B1]  …  [An-1, Bn-1]  [An, Bn],  каждый из которых содержит хотя бы одну из точек оптимума Х* функции  F(X).

Метод основан на делении текущего отрезка [а, B], Где содер­жится искомый экстремум, на две равные части с последующим выбором одной из половин, в которой локализуется максимум в качестве следующего текущего отрезка. Экстремум локализуется путем сравнения двух значений критерия оптимальности в точ­ках, отстоящих от середины отрезка на  /2, где  — погрешность решения задачи оптимизации.

Если F(х +  /2) > F(х -  /2), то максимум располагается на пра­вой половине текущего отрезка [а, B] , В противном случае — на левой.

Процесс поиска завершается при достижении отрезком [а, B] величины заданной погрешности  .

К недостаткам метода относится его работоспособность толь­ко для одноэкстремальных функций F(х) (т. е. таких, которые со­держат один экстремум того типа, который мы ищем в задаче), так как в других случаях при сравнении двух критериев в сосед­них точках невозможно правильно выбрать следующий интервал, где находится максимум.

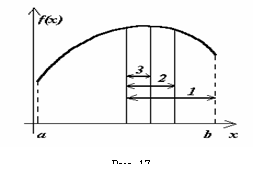
На рис. 17 приведены три этапа метода половинного деле­ния. Сплошными вертикальны­ми линиями отмечены середины отрезков, а пунктирными — вы­числяемые значения критерия оптимальности слева и справа на  /2 от середин.

Иллюстрация метода заключается в следующем: 1 – интервал, включающий в себя искомый максимум функции после первого этапа (первого деления пополам); 2, 3 – то же соответственно после второго и третьего этапов.

Существует и другой вари­ант алгоритма, заключающийся в следующем. После нахожде­ния середины отрезка (напри­мер, точка С1) В одной из полови­нок (допустим, в левой) находят среднюю точку (точка С2) и, срав­нивая значения функции в этих точках, определяют, в какой из половинок находится экстремум. Если F(c1)<F(C2), то в качестве следующего отрезка выбираем отрезок [а, с1], Если же F(c1)>F(C2), То берут новую точку в середине правой половины (точка С3) и в ней вычисляют функцию. В зависимости от сравнения зна­чений функции в точках С3 и С1 Выбирают новый отрезок [с1, B] Или [с2, с3] и т. д.

Второй вариант метода не имеет с точки зрения эффективно­сти принципиального отличия от первого, так как эффективность принято оценивать по наихудшему варианту (т. е. по двум вычис­лениям F(X) на каждом шаге). В первом варианте метода есть одна особенность, которая его делает очень эффективным при экспериментальном отыскании экстремума (например, при авто­матической настройке технических систем или при практическом поиске наилучших условий деятельности экономического объек­та). Малые отклонения от текущей точки обеспечивают в процес­се поиска отсутствие "шараханий", сопровождающихся резкими отклонениями состояния системы.

< Предыдущая		Следующая >