09. Условные вероятности. Независимость событий
Условная вероятность Р(В / А) = РA(В) - это вероятность осуществления события В при условии, что событие А уже произошло (причем последнее не является невозможным, т. е. Р(А) > 0). Эту вероятность можно вычислить по формуле
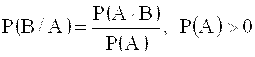
Для краткости эта величина называется “вероятностью события В при условии А”. Заметим, что для величины Р(В / А) выполняются аксиомы I, II, III, и, следовательно, простейшие свойства (см. §6).
Обозначим через Х число очков, выпавших при одном бросании игральной кости. Пусть А = {Х – простое число}, В = {Х – четное число}. Тогда Р(А) = 3/6 = 1/2 (числа 2, 3, 5 - простые, 1, 4, 6 - нет), Р(В) = 3/6 = 1/2, Р(А · В) = 1/6 (простое и четное одновременно число только одно - это 2). Следовательно, Р(В / А) = 1/3, т. е. вероятность того, что выпало четное число очков при условии, что выпало простое число очков, равна 1/3 (среди 3 простых чисел четное - одно); Р(А/В) = 1/3, т. е. вероятность того, что выпало простое число очков при условии, что выпало четное число очков, также равна 1/3 (среди 3 четных чисел простое - одно) .
События А и В называют независимыми, если
Р(А · В) = Р(А) · Р(В).
Если одно из событий невозможное ( Æ ), то в обеих частях стоят нули. Если же Р(А) > 0 и Р(В) > 0, то Р(А / В) = Р(А), Р(В / А) = Р(В).
Для последнего примера Р(А · В) ¹ Р(А) · Р(В) , значит, А и В зависимые.
Во многих задачах независимость событий задается по условию задачи (из общих соображений).
| < Предыдущая | Следующая > |
|---|