02. Развитие понятия «число»
Числа — это неотъемлемое орудие современной цивилизации, используемое для упорядочения сферы ее деятельности. В наиболее примитивном применении числа служат опознавательными знаками, будь то телефонные номера, номера автомашин или числа кода ZIP. На этом уровне мы просто сравниваем одно число с другим, не подвергая их арифметическим операциям. (Вряд ли можно ожидать, что получится что-либо значимое, если сложить номера телефонов Леонарда Бернстейна и Элизабет Тейлор.) На следующей, чуть более сложной ступени мы извлекаем пользу из естественного порядка положительных целых чисел, например, когда запоминаем номер нашей очереди к мясному прилавку или когда на скачках записываем наездников, приходящих к финишу. Здесь мы еще не нуждаемся в операциях над числами; все, что нас интересует, — это больше или меньше одно число, чем другое. Арифметика в полном смысле этого слова ПоявЛЯЕтся, лиШЬ когда задают себе вопрос: «Сколько?» Вот здесь нас уже ждут трудности вычитания, сложения, умножения, деления, извлеЧЕния квадратных корней и еще более замысловатых операций над числами.
Сложность цивилизации, как в зеркале, отражается в сложности Используемых ею чисел. Две с половиной тысячи лет назад вавилоняне довольствовались натуральными числами, подсчитывая принадлежащие им несколько овец; их удовлетворяла простейшая арифметика, нужная для регистрации движения планет. Сегодня экономисты-математики пользуются матричной алгеброй для описания взаимосвязей сотен предприятий, а физики — преобразованиями в гильбертовом пространстве (т. Е. числовой концепцией на семь уровней абстракции выше, чем натуральные числа) для предсказания квантовых явлений.
Числовые системы, применяемые в математике, могут быть расчленены на пять главных ступеней, от самых простых до самых сложных: 1) система, состоящая только из положителЬНых целых чисел; 2) более высокая ступень, включающая положительные и отрицательные целые числа и нуль; 3) рациональные числа, в которые дроби входят на равных правах с целыми числами; 4) действительные числа, включая иррациональные числа, такие, как, например, P, и 5) комплексные числа, вводящие в рассмотрение «мнимое число» ![]() .
.
Положительные целые числа — это те, что познает ребенок, когда учится считать. Обычно их записывают в виде 1, 2, 3, 4,..., но они могут быть представлены также множеством других способов. Римляне записывали их своими знаками I, II, III, IV, ... ; греки своими А, В, Г, D, ..., а в двоичной системе счисления, куда входят лишь символы 0 и 1, эти числа записывались бы как 1, 10, 11, 100, .... Все это суть вариации одного и того же: мы используем различные символы для обозначения неких сущностей, смысл и порядок которых понимаются однозначно.
В первобытном обществе человек нуждался лишь в нескольких первых числах, но с приходом цивилизации вынужден был изобретать все бОЛьшие и большие числа. Этот процесс развития чисел проходил с огромным трудом. Как заметил Бернард Шоу в своем «Человеке и Сверхчеловеке»: «Для бушмена, который не может вести счет, не прибегая к помощи своих пальцев, одиннадцать — неисчислимое количество». Еще в III в. до н. э. люди не умели выражать большие числа систематически; тогда-то Архимед предложил некий довольно затруднительный способ их именования в своем труде «Исчисление песчинок».
Греческие математики, которые бились над именованием больших чисел, совершили скачок от конечного к бесконечному. После четверки есть еще число, а после него еще одно, и так до бесконечности будут находиться целые числа. Для древних эта концепция представлялась весьма важным достижением творческой мысли и вдохновения, поскольку она шла вразрез со всеми накопленными данными в физике и с философскими воззрениями, что' Вселенная должна быть конечной. Смелая идея о бесконечности открывала широкие возможности в математике, но она в то же время приводила к парадоксам. Смысл понятия бесконечности и по сей день раскрыт не до конца.
Как ни странно, но еще труднее оказалось сделать шаг от положительных чисел к отрицательным. В наШИ дни, когда 10 градусов ниже нуля — это всеми однозначно понимаемая величина и когда каждому ребенку знаком обратный счет «..., 5, 4, 3, 2, 1, ...», отрицательные числа представляются совершенно ясным понятием. Но греки имели дело с отрицательными числами только в терминах алгебраических выражений для площадей квадратов и прямоугольников, например ![]() . Отрицательные числа были окончательно приняты в математике лишь после появления в 1545 г. «Ars МаGnа» Джироламо Кардано.
. Отрицательные числа были окончательно приняты в математике лишь после появления в 1545 г. «Ars МаGnа» Джироламо Кардано.
Дроби (или рациональные числа — название, под которым они фигурируют в теории чисел) древнее отрицательных чисел. Их можно найти в самых ранних математических записях, они весьма подробно обсуждаются в одном египетском папирусе, относящемся к 1550 г. до Н.Э. (папирусе Ринда). Нынешний способ записи дробей (например, ![]() ), так же как и современный способ арифметических действий над ними, восходит к XV — XVI Вв.
), так же как и современный способ арифметических действий над ними, восходит к XV — XVI Вв.
Иррациональные числа также имеют длинную историю. В VI в. до н. э. математическая школа Пифагора столкнулась с числом, которое нельзя было отнести ни к целым числам, ни к дробям. Это число, возникшее в связи с теоремой Пифагора, было ![]() — длина диагонали квадрата (или гипотенузы равнобедренного прямоугольного треугольника) со стороной, длина которой принималась за единицу. Греки были потрясены открытиЯМ, что значение
— длина диагонали квадрата (или гипотенузы равнобедренного прямоугольного треугольника) со стороной, длина которой принималась за единицу. Греки были потрясены открытиЯМ, что значение ![]() нельзя выразить в виде отношения
нельзя выразить в виде отношения ![]() с целыми А и B, или, иными словами, что
с целыми А и B, или, иными словами, что ![]() не равняется никакому рациональному числу. Так как они исходили из того, что числа бывают только рациональными, для них это открытие было равносильно тому, что такая диагональ вообще не имеет математической длины. Греки разрешили этот парадокс, приняв, что под числами и надлежит понимать длины. Но это мешало развитию алгебры и арифметики, и греческие математики попали в тупик.
не равняется никакому рациональному числу. Так как они исходили из того, что числа бывают только рациональными, для них это открытие было равносильно тому, что такая диагональ вообще не имеет математической длины. Греки разрешили этот парадокс, приняв, что под числами и надлежит понимать длины. Но это мешало развитию алгебры и арифметики, и греческие математики попали в тупик.
Понадобились века дальнейшего развития и усложнения в математике, чтобы осмыслить то, что корень квадратный из двух можно выразить с помощью десятичных дробей, если поставить многоточие после вычисленных десятичных знаков. Сегодня мы нажимаем на клавиш извлечения квадратных корней вычислительного устройства и на табло появляется ответ: ![]() = 1,41421.... С помощью электронных вычислительных машин таких точных десятичных знаков можно получить тысячи. Любое число, которое может быть записано в таком виде — одной или более цифр слева от запятой и бесконечной последовательностью цифр справа от запятой, — называют «действительным» числом. Таким путем мы можем выразить положительные Целые числа (например, 17 = 17.0000...), отрицательные целые числа( -3= -3,000...) или лЮБЫЕ рациональные числа (17
= 1,41421.... С помощью электронных вычислительных машин таких точных десятичных знаков можно получить тысячи. Любое число, которое может быть записано в таком виде — одной или более цифр слева от запятой и бесконечной последовательностью цифр справа от запятой, — называют «действительным» числом. Таким путем мы можем выразить положительные Целые числа (например, 17 = 17.0000...), отрицательные целые числа( -3= -3,000...) или лЮБЫЕ рациональные числа (17![]() = 17,25000...). Некоторые рациональные числа не приводят к бесконечной цепочке нулей справа от запятой; так, например, десятичное выражение для одной седьмой есть:
= 17,25000...). Некоторые рациональные числа не приводят к бесконечной цепочке нулей справа от запятой; так, например, десятичное выражение для одной седьмой есть: ![]() =0,142857 142857 142857.... Эти числа относятся к рациональным потому, что справа от запятой они содержат одинаковую беспрерывно повторяющуюся группу знаков. Иррациональными называют те числа, в десятичном выражении которых стоит, как мы видели в случае
=0,142857 142857 142857.... Эти числа относятся к рациональным потому, что справа от запятой они содержат одинаковую беспрерывно повторяющуюся группу знаков. Иррациональными называют те числа, в десятичном выражении которых стоит, как мы видели в случае ![]() , бесконечная непериодическая последовательность десятичных знаков. Наиболее Известны из иррациональных чисел
, бесконечная непериодическая последовательность десятичных знаков. Наиболее Известны из иррациональных чисел ![]() = 1,4142135623... и p = 3,1415926535 ... . Разумеется, иррациональные числа входят в совокупность действительных чисел.
= 1,4142135623... и p = 3,1415926535 ... . Разумеется, иррациональные числа входят в совокупность действительных чисел.
К комплексным числам мы переходим, когда сталкиваемся с числами, называемыми Мнимыми — термин, который сегодня лишь своеобразный реликт более наивной эры в арифметике. Величина ![]() характерна для комплексных чисел; при умножении на себя этой величины получается -1. Поскольку при этом нарушается основное правило, что при перемножении двух положительных или двух отрицательных чисел должно получиться число положительное, Величина
характерна для комплексных чисел; при умножении на себя этой величины получается -1. Поскольку при этом нарушается основное правило, что при перемножении двух положительных или двух отрицательных чисел должно получиться число положительное, Величина ![]() (или I, как ее обычно обозначают) действительно является странной, поскольку ее нельзя назвать ни положительной, ни отрицательной. «Мнимые числа, — писал в 1702 г. Готтфрид Вильгельм фон Лейбниц, — это поразительный полет духа божьего; это почти амфибии, находящиеся где-то между бытием и небытием». С эпохи Возрождения математики стали использовать комплексные числа (вида
(или I, как ее обычно обозначают) действительно является странной, поскольку ее нельзя назвать ни положительной, ни отрицательной. «Мнимые числа, — писал в 1702 г. Готтфрид Вильгельм фон Лейбниц, — это поразительный полет духа божьего; это почти амфибии, находящиеся где-то между бытием и небытием». С эпохи Возрождения математики стали использовать комплексные числа (вида ![]() ) для решения уравнений и открыли много прекрасных тождеств, хотя никто не мог объяснить, что это были за колдовские мнимости. Абрахам Де Муавр вывел формулу
) для решения уравнений и открыли много прекрасных тождеств, хотя никто не мог объяснить, что это были за колдовские мнимости. Абрахам Де Муавр вывел формулу ![]() Леонард Эйлер установил соотношение
Леонард Эйлер установил соотношение
(здесь Е — основание «натуральных логарифмов», равное 2,71828...).
Комплексные числа оставались для математиков лишь предметом отвлеченных манипуляций вплоть до XIX в,, когда математики начали искать для них конкретные представления. Норвежец Гаспар Вессель Первым ввел геометрическое представление комплексных чисел, это послужило основой для исключительно красивого математического построения, известного ныне как теория функций комплексного переменного. Позднее ирландский математик Уильям Роуэи Гамильтон развил алгебраическую интерпретацию Комплексных чисел, согласно которОЙ каждое комплексное число представлялось парой обычных чисел. Это помогло утвердить основание для развития аксиоматического подхода к алгебре.
В то же время физики установили, что комплексные числа пригодны для описания различных физических явлений. Эти числа начали входить в уравНЕния электростатики, гидродинамики, аэродинамики, теории колебаний и, наконец, в квантовую механику. Сегодня многие труды по теоретической физике и технике написаны языком комплексных чисел.
В XIX в. математики ввели еще несколько новых числовых систем. Из них три заслуживают особого внимания — кватернионы, матрицы и трансфинитные Числа.
Кватернионы - великое творенье Гамильтона. В течение многих лет ему не давал покоя тот факт, что умноЖЕние комплексных чисел можно представить просто как поворот на Плоскости. Нельзя ли ввести новый вид чисел и определить способ их умножения, выразив с помощью него поворот в трехмерном пространстве? Эти числа Гамильтон назвал триплетами. Точно так же, как Вессель представлял комплексные числа точками на двумерной плоскости, триплеты представляли точки трехмерного пространства.
Задача о триплетах, беспрестанно занимавшая Гамильтона, оказалась крепким орешком. Вся семья Гамильтона переживала с ним его неудачи. Сам он рассказывал, что стоило ему спуститься к завтраку, как один из его сыновей спрашивал: «Ну, папа, можешь ли ты уже умножать триплеты?» И папа должен был удрученно отвечать: «Нет, я могу только складывать и вычитать их».
Однажды в 1843 г., когда Гамильтон вместе с женой прогуливались вдоль канала в Дублине, он вдруг постиг способ умножения своих триплетов. Окрыленный успехом, он тут же вырезал перочинным ножом на Бруемском Мосту ключ к решению задачи; прохожие, должно быть, были озадачены, прочитав следующую запись: «![]() ».
».
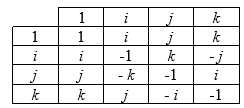
Буквы I, J и K означали гиперкомплексные числа, которые Гамильтон назвал кватернионами (общий вид кватерниона ![]() , где
, где ![]() и D Означают действительные числа). В точности так же как квадрат
и D Означают действительные числа). В точности так же как квадрат ![]() равен -1, так и
равен -1, так и ![]() . Загадка умножения кватернионов заключалась в том, что в нем не выполняется коммутативный закон умножения. В то время как в случае обычных чисел
. Загадка умножения кватернионов заключалась в том, что в нем не выполняется коммутативный закон умножения. В то время как в случае обычных чисел ![]() , при перестановке кватернионов произведение должно измениться, например
, при перестановке кватернионов произведение должно измениться, например ![]() , но
, но ![]() .
.
Таблица 1
Вторая новая числовая концепция, упомянутая выше, а именно понятие матрицы, была развита почти одновременно Гамильтоном и английскими математиками Дж. Дж. Сильвестром и Артуром Кэли. Матрицу можно рассматривать как прямоугольную таблицу чисел, например
![]()
Вся таблица мыслится как единый объект. При соответствующих обстоятельствах возможно определить операции сложения, вычитания, умножения и деления матриц. В результате появляется целая система объектов, свойства которых в чем-то сходны со свойствами обычных чисел; матрицы приносят огромную пользу во многих разделах чистой и прикладной математики.
Третья новая концепция — трансфинитные числа — представляет собой идею совсем иного рода. Эта идея очень занимательно изложена в фантастическом примере, который приписывается знаменитому немецкому математику Давиду Гильберту под названием «Отель Гильберта». Человек приходит в отель Гильберта и просит номер. «Гм, — отвечает администратор, — у нас свободных номеров нет, однако эта проблема разрешима; мы сможем найти Вам номер». С этими словами он помещает вновь прибывшего в комнату № 1, ее владельца переселяет в комнату № 2, жильца этой комнаты — в комнату № 3 и т. д. Занимающий комнату N оказывается в комнате N +1. Просто в этой гостинице бесконечное число комнат.
На основании чего же тогда администратор утверждает, что все номера заняты? Аналогичный парадокс подметил Галилей. Каждое целое число может быть возведено в квадрат, и отсюда вытекает, что квадратов столько же, сколько и самих чисел. Но возможно ли это, если вспомнить, что многие целые числа не являются квадратами других чисел, например 2, 3, 5, 6, ...?
Один из весьма заманчивых аспектов математики заключается именно в том, что самые тернистые ее парадоксы могут расцвести прекрасными теориями. В XIX в. немецкий математик Георг Кантор превратил изложенный выше парадокс в новую числовую систему и в арифметику бесконечных чисел.
Он начал с определения бесконечного множества как такого, которое может быть поставлено во взаимно однозначное соответствие с частью самого себя в точности так же, как целые числа находятся во взаимно однозначном соответствии со своими квадратами. Далее он заметил, что каждое множество, которое может быть поставлено в такое соответствие с множеством всех положительных целых чисел, должно содержать бесконечное число элементов; такое «число» он обозначил первой буквой древнееврейского алфавита «алеф» c. Это «первое количественное трансфинитное число» Кантор обозначил индексом «нуль». Затем он показал, что существует бесконечно много иных множеств (среди которых, например, множество всех действительных чисел), которые нельзя поставить во взаимно однозначное соответствие с множеством положительных целых чисел, поскольку они больше этого множества. Размеры таких множеств представляются другими трансфинитными количественными числами (![]() и т. д.). Из столь, казалось бы, несовершенного материала Кантор создал арифметику обычных и Трансфинитных чисел. В этой арифметике некоторые общепринятые ПраВила отвергаются, и мы сталкиваемся со странными уравнениями, такими, как
и т. д.). Из столь, казалось бы, несовершенного материала Кантор создал арифметику обычных и Трансфинитных чисел. В этой арифметике некоторые общепринятые ПраВила отвергаются, и мы сталкиваемся со странными уравнениями, такими, как ![]() . Это и есть записанный в символах парадокс с отелем.
. Это и есть записанный в символах парадокс с отелем.
Трансфинитные числа пока еще не нашли применения за пределами самой математики. Но в ней они оказали заметное влияние и стимулировали дальнейшую разработку множества логических и философских, построений. С появлением знаменитой Канторовой «Гипотезы континуума» возник целый ряд нерешенных проблем, которые до сих пор занимают математиков.
| < Предыдущая | Следующая > |
|---|