19. Интегрирование тригонометрических функций. Общие замечания о методах интегрирования
I. Интегралы типа ![]() , где т и п — целые числа.
, где т и п — целые числа.
А) Одно из чисел т или П — нечетно. В этом случае интегралы сводятся к интегралам от рациональных функций.
Метод интегрирования ясен из приведенных примеров.
Замечая, что ![]() , сделаем замену переменной:
, сделаем замену переменной: ![]() Это дает
Это дает ![]() и, следовательно, так как
и, следовательно, так как ![]() получим
получим
![]()
Пример 2. ![]()
Умножив числитель и знаменатель Подынтегрального выражения на ![]() получим
получим
![]() . Положим
. Положим ![]() тогда
тогда ![]()
![]()
![]()
Б) Оба ПоказатЕЛя т и N — четныЕ нЕОтрицатЕЛьные числа (в частности, одно из них может быть равным нулю). Заменяя ![]() и
и ![]() по формулам:
по формулам:
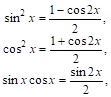
МЫ ДОбьемся того, что произведение ![]() заменится СумМой Произведений такого же вида, но с меньшими показателями СТепеней; метод интегрирования ясен из следующих примеров:
заменится СумМой Произведений такого же вида, но с меньшими показателями СТепеней; метод интегрирования ясен из следующих примеров:
Пример 1.
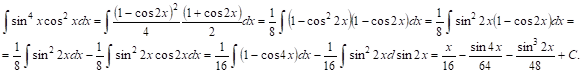
Пример 2.
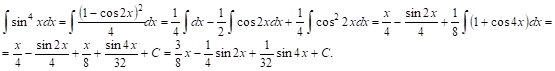
II. Интегралы типа
![]()
ЭТи интегралы вычисляются методом разложения на основании следующих тригонометрических тождеств:
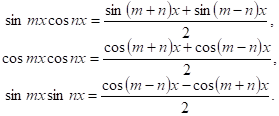
Пример 1.
![]()
Пример 2.
![]()
Рассмотрим интегралы типа ![]()
Где R — рациональная функция своих аргументов ![]() и
и ![]() . Такие интегралы называются Тригонометрическими. Например, интегралы
. Такие интегралы называются Тригонометрическими. Например, интегралы
![]()
Будут тригонометрическими интегралами, так как Подынтегральные функции являются рациональными функциями аргументов ![]() и
и ![]() . Наоборот, интеграл
. Наоборот, интеграл ![]() не является тригонометрическим, так как под интегралом стоит функция, не рацИОнальная относительно
не является тригонометрическим, так как под интегралом стоит функция, не рацИОнальная относительно ![]() и
и ![]() . Покажем, что всякий тригонометрический интеграл можно свести к интегралу от рациональной функции. Для этого вместо Х введем новую переменную Z, связанную с переменной Х соотношением
. Покажем, что всякий тригонометрический интеграл можно свести к интегралу от рациональной функции. Для этого вместо Х введем новую переменную Z, связанную с переменной Х соотношением ![]()
Тогда ![]() и
и ![]() выразятся рационально через Z. В самом деле, применяя формулы, известные из тригонометрии, имеем:
выразятся рационально через Z. В самом деле, применяя формулы, известные из тригонометрии, имеем: 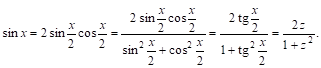
Аналогично, 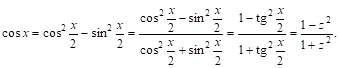
Наконец, учитывая, что ![]() найдем
найдем ![]() , ДифференЦируя, получим
, ДифференЦируя, получим ![]() .
.
Таким образом, если положить ![]() , то
, то
![]() (17)
(17)
Формулы (17) показывают, что ![]() ,
, ![]() и Dx рационально выражаются через Z, поэтому
и Dx рационально выражаются через Z, поэтому
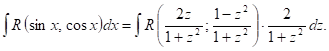
Последний интеграл является интегралом от рациональной функции переменного Z и может быть найден методами, рассмотренными ранее.
Приведем примеры.
Пример 1. ![]() Полагая
Полагая ![]() и применяя формулы (17), имеем:
и применяя формулы (17), имеем:
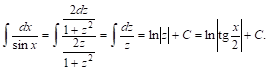
Пример 2. ![]() Полагая
Полагая ![]() находим
находим
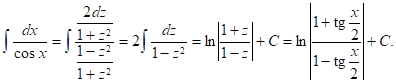
Заметим, что интеграл можно вычислить, если воспользоваться результатами предыдущего примера. В самом деле,
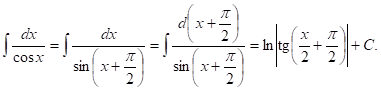
Хотя ответы по форме получились различными, однако, ЛЕгко показать, что
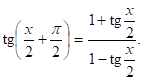
Пример 3. ![]() Применим указанную выше замену переменной, положив
Применим указанную выше замену переменной, положив ![]() . Тогда, согласно формулам (17), наш интеграл преобразуется следующим образом:
. Тогда, согласно формулам (17), наш интеграл преобразуется следующим образом:
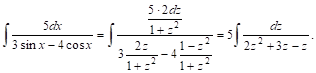
Разложим дробь ![]() на сумму простейших дробей:
на сумму простейших дробей: ![]()
Следовательно, 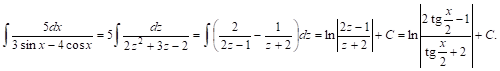
Подстановкой ![]() интегралы
интегралы ![]() всегда приводятся к. интегралам от рациональных функций. Однако это ведет порой к слишком громоздким вычислениям. В некоторых случаях эти вычисления можно упростить. Так, например, если
всегда приводятся к. интегралам от рациональных функций. Однако это ведет порой к слишком громоздким вычислениям. В некоторых случаях эти вычисления можно упростить. Так, например, если ![]() где Т И N целые числа, то удобнее пользоваться методами, изложенными в П. I.
где Т И N целые числа, то удобнее пользоваться методами, изложенными в П. I.
Укажем еще на один частный случай функции ![]() , при котором применение другой подстановки значительно сокращает вычисления.
, при котором применение другой подстановки значительно сокращает вычисления.
IV. ИнтЕГралы от функций, рационально зависящих от ![]()
![]()
Эти интегралы сводятся к интегралам от рациональной дроби, если СДелать замену переменной ![]() .
.
Подынтегральное выражение в последнем интеграле является рациональной функцией от Z.
Приведем пример:
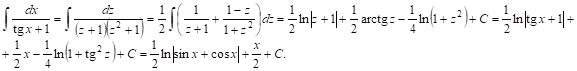
Замечание. Такой же подстановкой берется интеграл ![]() , если
, если ![]() и
и ![]() входят только в четных степенях. Это следует из того, что
входят только в четных степенях. Это следует из того, что ![]() и
и ![]() выражаются рационально через
выражаются рационально через ![]()
![]()
Пример:
![]() Мы разобрали наиболее важные методы интегрирования, охвАТывающие довольно обширный класс элементарных функций. Однако следует заметить, что на практике не всегда следует действовать по трафарету.
Мы разобрали наиболее важные методы интегрирования, охвАТывающие довольно обширный класс элементарных функций. Однако следует заметить, что на практике не всегда следует действовать по трафарету.
Так, например, интеграл ![]() можно было бы взять обычным методом интегрирования рационАЛьных функций, разложив Подынтегральную функцию в сумму простейших дробей:
можно было бы взять обычным методом интегрирования рационАЛьных функций, разложив Подынтегральную функцию в сумму простейших дробей:
![]()
Однако при внимательном рассмотрении Подынтегральной функции мы замечаем, что числитель ![]() является производной знаменателя. Поэтому
является производной знаменателя. Поэтому
![]()
ИскуССтво вычисления интегралов приобретается практикой при решении достаточно большого количества примеров.
Так как нахождение новых интегралов очень часто сводится к ранее известным, то для оБЛегчения можно рекомендовать пользование таблицами интегралов.
В заключение напомним, что далеко не всякий интеграл От Непрерывной элементарной функции может быть взят в элементарных функциях. Иначе говоря, хотя первообразная и существует в силу теоремы существования, но она не может быть выражена с помощью конечного числа алгебраических действий и суперпозиций, проведенных над элементарными ФункЦиями.
При изучении различных методов Интегрирования мы уже всТРечались с такими интегралами. Ранее, например, было указано, что функции ![]() ,
, ![]() ,
, ![]() не интегрируются в элементарных функциях.
не интегрируются в элементарных функциях.
Часто бывает важно изучить свойства тех функций, которые являются первообразными от некотОРых элементарных функций, но сами не выражаются через элементарные функции. Рассмотрим несколько примеров таких функций.
Пример 1. Та первообразная от функции ![]() , которая удовлетворяет дополнительному условию: ее значение при Х = 0 равно нулю — называется интегральным синусом и обозначается si Х.
, которая удовлетворяет дополнительному условию: ее значение при Х = 0 равно нулю — называется интегральным синусом и обозначается si Х.
Таким образом,
![]() или
или ![]()
Где под si Х подразумевается та первообразная, которая удовлетворяет условию si 0 = 0.
Пример 2. Интегральным косинусом ![]() называется та первообразная от
называется та первообразная от ![]() , которая удовлетворяет условию
, которая удовлетворяет условию ![]()
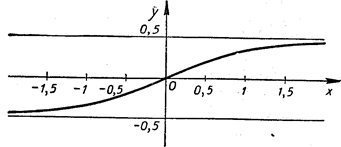
Пример 3. Большое значение в различных приложениях имеет первообразная Ф(Х) от функции ![]() удовлетворяющая дополнительному условию Ф (0) = 0. Эта функция встречается, в частностИ, в теории вероятностей и называется интегралом вероятности. Ее график представлен на рис. 1.
удовлетворяющая дополнительному условию Ф (0) = 0. Эта функция встречается, в частностИ, в теории вероятностей и называется интегралом вероятности. Ее график представлен на рис. 1.
Пример 4. Эллиптическими интегралами 1-го и 2-го рода называются такие первообразные от функций:
![]() где
где ![]()
Эти функции встречаются при вычислении длины дуги эллипса, откуда и происходит их название (эллиптические интегралы).
Все эти функции, а также многие другие функции, получаются подобным образом, хорошо изучены и для них составлены подробные таблицы, помогающие практически использовать эти функции.
| < Предыдущая | Следующая > |
|---|