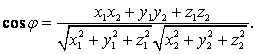3.1.6. Скалярное произведение

Пусть даны векторы А и B. Обозначим через φ угол между этими векторами. Скалярным произведением векторов А и B называется величина

Ab = |A||B| cos φ.

Векторы А и B называют Ортогональными (при этом пишут А ^ B), если угол между ними прямой. Нулевой вектор считается ортогональным любому. Из определения скалярного произведения вытекает, что

Ab = 0 Û A ^ B

(символом Û обозначается эквивалентность утверждений).

Остановимся на основных свойствах скалярного произведения.

1. Ab = ba.

2. (λA)B = λ(Ab).

3. Ab = |A| прА b.

4. A(B + c) = Ab + ac.

Доказательство.

В силу свойства 3 и (6)

A(B + c) = |A| прA (B + c) = |A|(прA B + прA C) = |A| прA B + |A| ПрA C = ab + ac.

5. Скалярным квадратом вектора А называется величина А2 = Аа. Из определения скалярного произведения получаем

А2 = |A|2. (8)

6. Если A = (X1,Y1,Z1) и B = (X2,Y2,Z2), то

Ab = x1X2 + Y1Y2 + Z1Z2.

Доказательство.

Имеем

Ab = (X1 i + y1 J + z1 K)( x2 i + y2 J + z2 K) = X1X2 I2 + Y1X2 Ji + Z1X2 Ki + X1Y2 Ij +

+ Y1Y2 J2 + Z1Y2 Kj + X1Z2 Ik + Y1Z2 Jk + Z1Z2 K2.

Поскольку Ij = Ik = Jk = 0, I2 = J2 = K2 = 1, получаем

Ab = x1X2 + Y1Y2 + Z1Z2.

7. Если A = (X,Y,Z), то

Доказательство.

Из свойств 5 и 6 получаем

Из равенства (7) и свойства 7 вытекает, что направляющие косинусы связаны соотношением

Cos2 α + cos2 β + cos2 γ = 1.

8. Если A = (X1,Y1,Z1) и B = (X2,Y2,Z2), а φ – угол между векторами А и B, то

Доказательство.

Из свойств 6 и 7 получаем

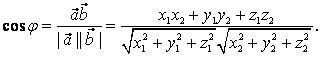
9. Если A = (X1,Y1,Z1) и B = (X2,Y2,Z2), то

ПрB A =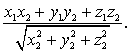

Доказательство.

Обозначим через φ угол между векторами А и B. Тогда из свойства 8 получаем

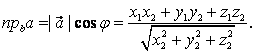
Рассмотрим выражение (A + b)2. Имеем

(A + b)2 = (A + b)(A + b) = A2 + 2Ab + B2.

Пользуясь равенством (8) и определением скалярного произведения, получаем

|A + B|2 = |A|2 + 2|A||B| + |B|2, (9)

Где φ – угол между векторами А и B. Рассмотрим треугольник с вершинами в

Точках А, В и С.

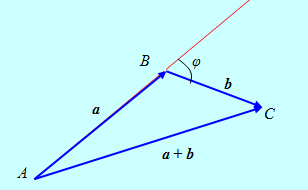
Рис. 11

Пусть А = B = Тогда = A + B. Положим α = R АВС. В силу того, что α = π – φ, cos α = - cos φ. Поэтому из (9) получаем известную теорему косинусов:

Пример 2. Даны координаты вершин треугольника A = {1, 1, 2},

B = {1, 6, 3} и C = {4, 5, 2}. Найти координаты проекции точки В на сторону АС.

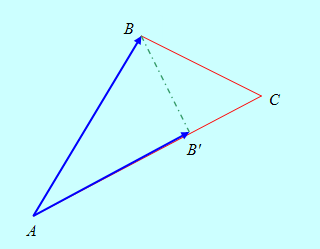
Рис. 12

Обозначим проекцию точки В на сторону АС через В′. Тогда

Имеем

Поэтому

Следовательно,

Отсюда

Упражнение 1.

В треугольнике с вершинами в точках A = {1, -2, 3},

B = {2, -2, 3} и C = {2,0,3} найти угол между медианой, проведенной из вершины А, и стороной АВ.

Решение

Найдем координаты вектора

Пусть точка М – середина стороны ВС, тогда

Найдем косинус искомого угла:

< Предыдущая		Следующая >